Self-potential (SP) surveys measure naturally occurring differences in electrical potential in the absence of artificial sources and have been applied to various fields since the first application in mineral explorations. Among various causes of SP occurrences, streaming potential is generated by the flow of groundwater, and makes SP surveys suitable for the exploration of groundwater table fluctuation, fractures, sinkholes and landslide occurrences. Recently, there has been many studies that applied SP surveys to monitor water leakage through dikes and embankments. In this review paper, we first review the characteristics and theoretical backgrounds of streaming potential in saturated or unsaturated porous media to introduce it in the embankment among various application field. After the review of the background theory, we review the past cases of field SP surveys on dikes and embankments and also the characteristics of field streaming potential data in the surveys. Further, by analyzing past studies of qualitative as well as quantitative interpretation of SP survey data, we show the possibility of quantitative interpretation of streaming potential data obtained on dikes and embankments. Consequently, it is hope that this review paper helps researches on SP surveys on dikes and embankments, and provides basis for interpretation methods of the SP data to identify leaked area and further leakage rate (or permeability).

Keywords: self-potential, streaming potential, embankment, dike, leakage, monitoring

최근 저수지, 호수, 강변, 바다에 위치하고 있는 수리시설물의 안전 및 누수 모니터링에 대한 중요성이 높아지면서 물리탐사 및 지질 공학적 방법을 활용하여 누수를 분석한다. 국내에서는 수리시설물의 안정성을 모니터링하기 위해 정기적으로 정밀 안전진단 지질조사를 수행하는데, 경제적 및 시간적 측면에서 물리탐사 방법이 보다 효과적이며 일반적으로 전기비저항 탐사 방법을 활용하고 있다(Lim, 2018). 전기비저항 탐사는 시추공을 활용한 지질 조사 보다 상대적으로 넓은 영역에서의 결함 부위, 침투수 이상대 및 제체 내 세굴현상 등과 같은 잠재적 취약대를 평가할 수 있지만(Song et al., 2005), 3차원(3D) 구조의 수리시설물에 의해 해석의 왜곡이 발생하는 등의 한계가 있다(Cho and Yong, 2019).
수리시설물 모니터링을 위해 전기비저항 탐사법 외에도 흐름 전위(streaming potential)에 의해 발생한, 자연적 전위 분포 차이를 측정하는 자연전위(Self-potential, SP) 탐사법이 많이 활용되었다(Butler and Llopis, 1990; Bièvre and Norgeot, 2005; Bolève et al., 2011; Kang et al., 2014; Wang et al., 2018). 자연전위 탐사는 지하의 수리 및 전기 화학 반응으로 인해 별도의 전류 송신원 없이 자연적으로 발생한 전위 차이를 측정하는 수동적인 탐사법이다. 이러한 자연전위는 전기이중층을 형성하고 있는 다공질 매질에서 지하수 흐름에 의해 발생하는 흐름 전위(Jouniaux et al., 2009; Song and Nam, 2018)와 이온의 확산, 산화 환원 반응, 양이온 흡착 등의 전기화학적 요인에 의한 자연전위로 나눌 수 있다.
특히 흐름 전위는 유체 흐름에 의해 발생하므로 유체 유동 특성을 분석하는 데 장점이 있다. 이에 따라 수리시설물 누수 평가(Ritter et al., 2015) 외에도 온도 기울기에 의한 지하수 흐름이 나타나는 지열 발전 분야(Perrone et al., 2004; Byrdina et al., 2014), 지하수 유동 및 균열 분석(Revil et al., 2004), 싱크홀 및 산사태 지역에서의 지하수 분포 해석(Jardani et al., 2007a; Giampaolo et al., 2016) 등의 다양한 분야에서 흐름 전위가 활용되었다. 전기화학적 자연전위는 쓰레기 매립지나 유류 오염지와 같은 이온 불균형이 발생하는 오염지(Giampaolo et al., 2004; Minsley et al., 2007a; Yu et al., 2019)나 황화 광체(Sato and Mooney, 1960; Biswas, 2017)에서 주로 활용되었다.
자연전위 탐사는 송신원 없이 자료를 취득할 수 있으므로 수리시설물의 모니터링에 장점이 있다. 누수가 발생하는 영역은 유체 흐름이 상대적으로 강하게 나타나므로 누수 영역에서 보다 뚜렷한 흐름 전위 이상을 관측할 수 있다. 국내에서도 수리시설물에서 누수를 관측하기 위해 자연전위 탐사를 수행하였는데(Song et al., 2000; Song et al., 2002 and 2005; Kang et al., 2014), 주로 2차원(2D) 측선에서의 정성적인 변화를 분석하거나 수치 시뮬레이션 결과와 현장 자료를 비교하여 누수를 해석하였다.
수리시설물에서 효과적으로 흐름 전위를 해석하기 위해 인위적으로 환경을 변화하여 정성적으로 누수 영역에서의 뚜렷한 이상 관측(Butler and Llopis, 1990; Bolève et al., 2011)과 함께 수리∙전기 시뮬레이션을 통한 정량적 해석에 대한 연구가 꾸준히 진행되었다. 흐름 전위 신호를 정량적으로 구현하기 위한 흐름전위 모델링은 Sill(1983)을 시작으로 수행되었고 Bolève et al.(2007)는 불포화대에서의 지하수 흐름에 의한 흐름 전위 신호를 고려할 수 있도록 하였다. 흐름전위 모델링을 통한 유동 전위 반응을 구현하는 것 뿐만 아니라 역산을 통해 지하의 유동 전류 밀도 분포와 누수 속도를 역해석하는 연구들도 많이 수행되고 있다(Rocyzki et al., 2006; Minsley et al., 2007a,b; Jardani et al., 2006, 2007a,b and 2008; Bolève et al., 2011).
이 논문은 흐름 전위 반응 특성 및 다양한 적용 분야를 소개한 이전 연구(Song and Nam, 2018)의 연장으로, 다양한 적용 분야들 중에서 수리시설물에서의 누수에 의한 흐름 전위의 적용 및 해석 사례를 분석하였다. 이를 위해 흐름 전위 발생 매커니즘과 정량적 해석을 위한 흐름 전위 모델링 및 탐사 자료의 역산법에 대해 먼저 설명하였다. 수리시설물에서의 자연전위 현장 탐사 특성에 대해 알아본 뒤, 수리시설물에서 일반적으로 나타나는 흐름 전위 반응의 특징에 대해 분석하였다. 마지막으로 대표적인 사례들을 중심으로 정성적 해석과 최근 활발히 연구되고 있는 정량적 해석 방법들을 소개하고 그 결과에 대하여 논하였다. 이 기술 보고를 통해 수리시설물에서의 흐름 전위 모니터링 연구에 대한 기초를 마련하고자 한다.

흐름 전위는 지하수 유동에 의해 발생하며 포화 상태 및 유체 흐름 특성에 따라 흐름 전위 크기에 영향을 미친다. 이 장에서는 흐름 전위 발생 이론, 흐름 전위 분포의 수치적 모델링과 자연전위 탐사 자료의 역산에 대해 설명한다.

2.1. 지하수 유동에 의한 흐름 전위 이론
흐름 전위는 대전된 다공질 매질 표면의 전기 이중층(또는 삼중층) (Ishido and Mizutani, 1981; Morgan et al., 1989)에서 확산층을 중심으로 하는 유체 흐름으로부터 발생하는 자연전위이다(Fig. 1). 포화 상태의 다공질 매질에서 흐름 전위는 전기적, 수리적 현상을 설명하는 각각의 연속방정식을 연계하여 설명할 수 있다(Bolève et al., 2007). 먼저 전기적 현상은



로 표현되며, 여기서 j는 전류밀도(current density) [A/m²], σ는 다공성 매질의 전기전도도(electrical conduc- tivity) [S/m], φ는 전위(electrical potential) [V], L은 흐름 전류 결합 계수[m²/(V s)], p는 공극수압 [Pa], ρ_f는 공극수의 밀도[kg/m³], g는 중력가속도[m/s²]이다.
한편 수리적 현상은



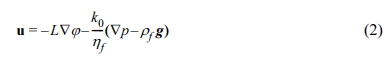
로 설명할 수 있으며, 이때 u는 Darcy velocity [m/s], k₀는 다공성 매질의 고유 유체 투수율(intrinsic permea- bility) [m²], η_f는 공극수의 동적 전단 점성(dynamic shear viscosity) [Pa·s]이다. 위 두 식에서의 수리전기적 결합 항들은 모두 흐름 전위와 전기 침투(electro-osmosis)와 같은 계면 동전 현상(electrokinetic phenomenon)을 설명한다. 계면 동전 현상은 지하의 미세한 입자 및 다공질 매질 표면이 대전되어 있을 때 공극수 내 이온이 매질 표면에 흡착 및 대전하여 전기적 이중층을 형성하고 전기적 평형 상태가 되는데 이 때 중력장 혹은 전기장에 의해 발생하는 현상들을 모두 포함한다. 전기 침투는 전기장에 의해 다공성 매질 내의 유체가 흐르는 현상으로 흐름 전위와 반대되는 개념이다. 식 (1)의 우항 -L(∇p - ρ/g)는 흐름 전류 밀도, j_s를 나타내며, 식 (2)의 첫 항 -L∇φ는 전기 침투 현상을 설명한다.
유동현상과 전기현상의 결합을 위해 정의되는 흐름 전위 결합 계수(C) [V/Pa]는 다음과 같이 표현될 수 있으며,



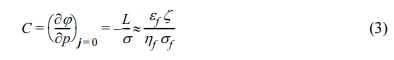
여기서 ε_f와 σ_f는 각각 공극수의 유전 상수[F/m]와 전기전도도이며, {{{EQUATIONS}}}는 지하 매질과 공극수 경계면의 주요 전기화학적 특성인 제타 전위[V]이다. C는 Helmholtz-Smoluschowski 식(Ishido and Mizutani, 1981; Morgan et al., 1989)과 관련하여 ζ와(Kosmulski and Dahlsten, 2006; Leroy and Revil, 2009) 연관이 있는데(식 (3)의 마지막 항), 매질 표면의 전기전도도를 무시할 수 있는 경우 C는 다공성 매질의 특성에 의존하지 않는다(Bolève et al., 2007).
전기 침투 효과(식 (2)의 첫 항)는 누수 속도와 관련하여 Revil and Linde(2006)에 의해 고려된 바 있지만, 전기장을 형성하는 외부의 전류원이 없다고 가정할 때 전기 침투 효과를 무시할 수 있다(Sill, 1983; Revil et al., 1999). 이에 따라 누수 속도(식 (2))는 다음과 같이 정리할 수 있다.



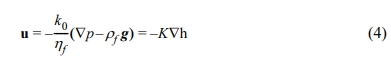
여기서 K는 수리 전도도(hydraulic conductivity) [m/s], h는 수두(head) [m] 이다(Bolève et al., 2007). 식 (4)는 포화 상태에서의 Darcy 법칙이며, 불포화 상태에서 유체 흐름은 van Genuchten 매개변수화(parametrization)를 고려하여 Richard 식을 이용하여 풀 수 있다.
전류 밀도에 대한 연속방정식(식(1))은 Nernst-Planck 식으로부터 전기장과 유동 속도로 다음과 같이 표현할 수 있다(Revil and Leroy, 2004; Revil and Linde, 2006).



여기서 E는 전기장이며(E = -∇φ) [V/m], Q̅v는 전기 이중층의 확산층에서의 단위 공극 부피 당 과전하 [C/m³]이다. 이 때 식 (5)에 우변의 두번째 항이 흐름 전류 밀도, j_s이다. 준정적 상태에서의 전하에 대한 연속방정식



를 고려하면, 식 (5)를 적용하여 흐름 전위 송신원에 대한 포아송 식으로 정리할 수 있다.



이 때, 흐름 전위 송신원, S͞͞는



로 부피당 전류 소스 밀도(volumetric current source density) [Am^-3]이다. (7) 식의 포아송 방정식의 소스는 누수 속도에 의해 설명할 수 있으며 해당 방정식의 해로 흐름 전위 신호 분포를 알 수 있다(Sill, 1983). (7)식으로부터 전위 분포가 지하의 전기전도도 분포 변화에도 크게 영향을 받는 것을 알 수 있다. 또한 정상 상태에서는 ∇·u=0이므로, 송신항은



으로 나타낼 수 있다.

2.2. 불포화상태에서의 흐름 전위
불포화대에서 흐름 전위는 지하수위 상부의 모세관의 존재와 불포화대 내에서의 유체 흐름에 의해 발생할 수 있다(Bolève et al., 2011). 불포화대에서 유체 흐름은 van Genuchten 매개변수화(parametrization)와 아래의 Richard 식을 이용하여 풀 수 있다.



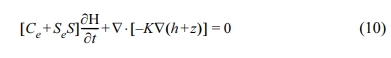
여기서 C_e는 비수분용량 [1/m]이며 수두(h)와 함수량(θ)으로 아래와 같이 계산할 수 있다.



함수량은 비포화도(relative saturation, S_w)와 매질 내 연결된 총 공극으로 나타낸다.



S는 저류계수[1/m], S_e는 유효 포화도로 잔여 포화도, S^r_w(residual saturation of water phase)와 비포화도(S_w)와 다음과 같은 관계가 있다.



한편 수리전도도, K는 상대투수율(relative permeability; k_r)과 포화상태의 수리전도도(K_s)로 다음과 같이 나타낼 수 있다.



Richard 식(식(10))을 푸는 데 필요한 변수들인 S_e, C_e, k_r, θ는 van Genuchten 매개변수 실험식(van Genuchten 1980; Mualem 1986)을 통해 특정 토양 별 불포화 상태에서 다음과 같이 정의하였다. 아래의 식에서 H는 지하수위(z_wt)와 일정 심도(z) 간 차이이며(z는 깊이 방향으로 양의 값), 지하수위에서 H는 0이다.



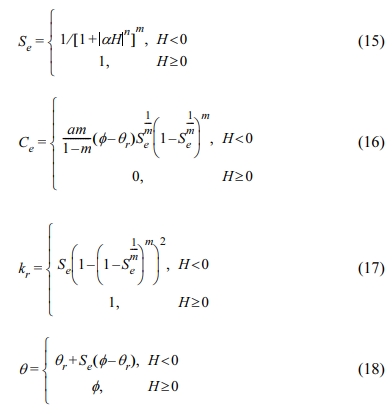
위의 식에서 θ_r는 잔여 함수량으로



이며, α, n, m은 다공성 매질의 특성을 결정하는 변수 값이다(van Genuchten, 1980; Mualem, 1986).
흐름 전류 밀도(streaming current density; j_s)는 유체 흐름 종류(점성 혹은 관성 층류)에 영향을 받는데(부록 A), 점성 층류일 때의 j(총 전류 밀도) 식(5)를 불포화 상태를 가정한 식으로 다음과 같이 표현할 수 있으며(Revil et al., 2007),



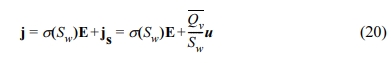
여기서 u는



이다. 한편, 불포화 상태에서의 전기비저항은 암석의 포화 정도에 따른 전기비저항 변화를 경험적으로 계산한 제 2 Archie식을 이용하여 계산할 수 있다(부록B).

2.3. 흐름 전위 반응 모델링 및 역산
유체 흐름에 대한 흐름 전위를 해석하기 위해서는 수치 모델을 통해 정량적으로 흐름 전위를 구현하고 환경 변화에 따른 흐름 전위 추이를 분석하는 것이 필요하다. 이를 위해 실제 현장을 모사한 수치 모델을 구성하고 포화 혹은 불포화대에서의 흐름 전위의 정의에 따라 모델링을 수행함으로써 흐름 전위 반응을 분석할 수 있으며, 현장에서 취득한 자연전위 자료를 역산하여 유체 흐름을 역해석할 수 있다. 수리시설물에서 취득한 자연전위 현장 자료의 정량적 해석을 위해 실제 현장 및 수치 모델에서 효과적으로 적용된 흐름 전위 모델링 및 역산 방법을 정리하였다(Fig. 2)(Bolève et al., 2009, 2011 and 2012; Rittgers et al., 2015).

- 모델링
포화대를 대상으로 하는 경우에는 Darcy 식(식(4)), 불포화대를 함께 고려하는 흐름 전위 모델링을 수행할 때는 Richard 식 (식(10))을 이용하여 수두 분포를 계산한다. 이 때 불포화 상태에서의 매질의 물성은 van Genuchten 매개변수를 이용하여 설정하고 경계 조건은 댐의 측면 경계와 바닥에서의 수두를 일정하게 한다. Darcy 식 혹은 Richard 식으로부터 얻어진 수두 분포를 기반으로 포아송 식(식(7))을 계산하여 S͞͞를 구한다. 이 때 지표에서의 전기적 흐름이 없도록 경계조건을 설정하고 계산 영역의 전기전도도 분포도 설정해주어야 하므로, 자연전위 해석 시 전기비저항 자료도 함께 고려하는 것이 중요하다(Jardani et al., 2008). 전기비저항 탐사를 자연전위 탐사와 동일한 측선에 대해 수행한 경우, 해당 전기비저항 자료를 자연전위 자료 역해석 시 사용할 수 있다.
- 역산
자연전위 역산은 포아송 방정식을 그린 함수를 이용하여 적분하고 중첩의 원리(principle of superposition)를 통해 측정된 자연전위 신호와 전류 소스 밀도 간의 선형 관계를 바탕으로 수행한다.



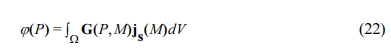
여기서 φ(P)는 P에서 측정된 자연전위, j_s(M)는 소스 점, M에서의 전류 소스 밀도, Ω는 지하수 흐름이 발생하는 소스 부피, dV는 인근의 요소 부피, G는 선형 사상 함수(linear mapping function)이며 각 성분은 그린 함수이다. 자연전위 탐사 시 지하수 흐름이 거의 없는 건조한 영역에 기준 전극을 위치시키므로, 그린 함수 계산 시에는 기준 전극 위치에서의 전위가 0이 되도록 모든 그린함수 요소에 적용될 수 있도록 하는 것이 중요하다. G는 전기비저항이 균일하다고 가정했을 때, 다음과 같이 간단하게 정의할 수 있다.



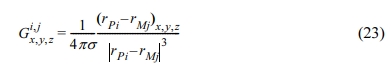
여기서 (x,y,z)는 3D 데카르트 좌표, r_Pi와 r_Mj는 각각 측정점, P_i의 위치와 소스점, M_j의 위치를 의미한다. 위의 식(23)로부터 지표 근처에 소스가 있는 경우 G의 값이 매우 커져 역산 수행 시 이에 대한 보정이 필요하다.
자연전위 역해석 수행 시 목적 함수(ψ)는



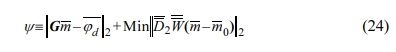
이며, 첫번째 항은 자료 오차항으로 II·I₂은 L₂ 노름(Euclidian norm), m̅은 3D 소스 전류 밀도 벡터, φ͞͞ _d는 지표 혹은 시추공에서 측정된 자연전위 자료 벡터이다. 자료 오차 항과 더불어 평활화 모델 제한 조건을 추가하여 해가 부드럽게 변할 수 있도록 한다(Jardani et al., 2006, 2007a,b; Bolève et al., 2009). 지표 근처 소스에 대한 보정은 평활화 조건 내에 심도에 따른 가중치(W̅₂)를 주어 지표 근처 소스의 값에 대한 보정을 수행한다. 이때, 2차 도함수의 이산 근사(discrete approximation)인 D̅₂는



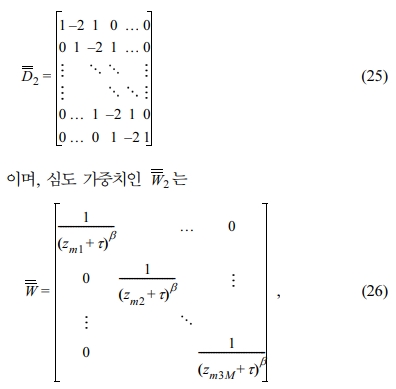
이다. W̅에서 t 는 작은 상수 값으로 z 값이 0에 가까워질 때 발산하지 않도록 하며 β 도 민감도 분석을 통해 0.85 또는 0.9의 상수값으로 사용되었다(Boulanger and Chouteau, 2001; Chasseriau and Chouteau, 2003). m̅₀는 이전 모델로, 계산 영역 내 매질의 물성을 가정하고 수리 문제를 풀어 구한 흐름 전위 분포를 사용하거나 전기비저항 탐사 자료 역산을 통해 얻은 전기비저항 구조에 대해 모델링한 흐름 전위 반응을 사용한다.

수리시설물에서 자연전위 탐사는 댐 환경 또는 관심 영역에 따라 2D 또는 3D 탐사를 수행한다. 3장에서는 수리시설물에서의 자연전위 탐사 수행 시 사용하는 전극 배열의 특성, 탐사 위치 별 탐사법 특성, 사용 가능한 전극의 종류 및 탐사 장비에 대해 소개하고자 한다.

3.1. 전극 배열 특성
자연전위 탐사 시 전극 배열에는 기준 전극을 중심으로 다른 전극에서 전위 차를 측정하는 기준점 고정법(fixed-based method)과 일정한 전극 간격으로 떨어진 전극 쌍에서 전위 차를 측정하는 방법(leap-frog or gradient method)이 있다(Fig. 3). 일반적으로 기준점 고정법 자료가 신뢰도가 높아 많이 활용된다. 수상 탐사의 경우에는 탐사의 편의성을 위해 배를 활용하여 2개의 비분극 전극 쌍을 끌고가며 전위 차를 측정하는 탐사법을 적용한다.
자연전위 탐사에서 기준 전극은 자연전위 이상이 나타나지 않는 높고 건조한 곳에 설치하여야 한다(Wang et al., 2018). 즉, 호수나 강에서 탐사할 때는 기준 전극을 상류에 설치하거나(Butler and Llopis et al., 1990; Wang et al., 2018), 수리시설물에서는 탐사 측선 가운데에서부터 2 km 떨어진 곳 혹은 탐사 측선 상부에 기준 전극을 설치하는 것이 좋다(Ikard et al., 2014; Kang et al., 2014). 그러나 탐사 편의를 위해 측선 중간에 전극을 추가로 설치하고 이를 기준 전극으로 활용하거나(Bolève et al., 2011), 사면 전체를 대상으로 탐사할 때에 제체 사면 중간이나 제체 끝에 기준 전극을 설치하여 성공적으로 탐사를 수행한 사례도 있다(Bolève et al., 2009; Moore et al., 2011; Rittgers et al., 2015). 또한, 제체 내 중심 코어 상부에 영구적으로 매립된 전극을 기준전극으로 활용하기도 한다(Dahlin et al., 2001). 한편 여러 개의 측선에서 자연전위 탐사를 할 때에 측선 마다 새로운 기준 전극을 설치할 수도 있는데, 이러한 경우에는 인접한 측선의 기준 전극 사이의 전위 차이를 측정한 뒤 이를 보정해주어야 한다(Minsely et al., 2008 and 2011).

3.2. 탐사 위치에 따른 탐사 특성
육상 제체 탐사 수행 시, 제체 상부에 2D 측선을 설치하거나 제체 사면 전체에 걸쳐 일정 간격으로 전극을 설치하여 탐사를 수행하는 것이 일반적이다(Bolève et al., 2009 and 2011; Moore et al., 2011; Minsley et al., 2011). 상황에 따라서는 여러 전극을 미리 설치하기 보다는, 2개의 전극만을 활용하여 전극을 옮겨가며 측정해도 의미 있는 결과를 얻을 수 있다(Dahlin et al., 2001; Panthulu et al., 2001; Ikard et al., 2014). 전극 간격은 가탐 심도에 영향을 주는 전기비저항 탐사와 같이 민감하지 않으며 탐사 영역에 따라 일정 간격으로 측정하며 관심 영역에 대해서는 보다 작은 간격으로 탐사를 수행할 수 있다(Jardani et al., 2006). 지표 탐사와 별도로 지전류(telluric current) 모니터링을 위해서, 제체 내부의 중심 코어 상부에 비분극 전극을 영구적으로 매립할 수도 있다(Dahlin et al., 2001).
수상에서 탐사를 수행할 때는 배를 활용하여 얕은 심도에서 전극을 바닥에 끌고 가며 탐사를 수행할 수도 있는데, 이 때는 주로 스트리머(streamer)를 이용하여 5~15 m 간격으로 고정되어 있는 쌍극자를 끌고 가며 일정 간격에 따라 전위 차를 측정 방법을 활용하여 탐사를 수행한다(Dahlin et al., 2001; Blèvre and Norgeot, 2005; Bolève et al., 2012). 전극의 쌍극자 방향에 따라 자연전위 자료에 영향을 많이 줄 수 있으므로 다양한 방향에 대해 탐사를 수행한 뒤 보정해야 한다(Dahlin et al., 2001).

3.3. 전극 종류 및 측정 장비
흐름 전위는 자료의 세기가 현장에 따라 수 mV에서 수십 mV 범위로 작고 주변 환경에 의한 잡음의 영향을 많이 받기 때문에 대체로 비분극 전극을 활용하여 탐사를 수행한다. 자연전위 탐사에 많이 활용되는 비분극 전극에는 Cu-CuSO₄ 비분극 전극, Pb-PbCl₂ 전극(Petiau 전극) 등이 있다(Petiau, 2000). Pb-PbCl₂ 전극은 연간 자료 변화가 적어 모니터링에 보다 효과적이며, Cu-CuSO₄ 전극은 온도 변화에 민감하여(1.2 mV/^oC) 토양과 접촉하는 비분극 전극의 다공성 매질과 주변 토양 간 온도 평형을 위해 10분 이내의 시간이 소요된다(Jardani et al., 2006). 국내에서도 위의 비분극 전극 특성들을 반영하여 비분극 전극을 제작하여 현장 적용을 위해 검증한 바 있다(Song, 2001).
비분극 전극이 아닌 구리로 코팅한 철 전극(Copper clad steel grounding rods) 또는 스테인리스 전극을 활용하여 탐사를 수행할 수도 있다. 이러한 전극에서는 온도에 의한 영향 뿐만 아니라 전극 분극 등의 발생으로 잡음이 더 발생하므로 지속적인 모니터링을 통해 주변 환경 변화에 따른 잡음 분석도 함께 수행해야 하기 때문에(Butler and Llopis, 1990; Kang et al., 2014), 비분극 전극을 사용하는 것이 보다 안정적이다. 특히 온도 변화는 비분극 전극과 그 외의 전극 모두에 많은 영향을 미치는 인자 중 하나인데, 이에 대한 영향을 최소화하기 위해서는 지표에서 수~수십 cm 이상 혹은 완전히 전극을 묻는 것이 안정적이다(Corwin 1989).
비분극 전극을 땅에 설치할 때 땅과의 접촉 저항을 낮춰줄수록 향상된 신호를 얻을 수 있는데, 이를 위해 염도를 높인 벤토나이트 진흙(salted bentonite mud)을 활용하여 접촉 저항을 효과적으로 낮출 수 있다(Minsley et al., 2011; Wang et al., 2018). 또한 한 측점에 3개의 전극을 설치하고 전극 당 각각 5회씩 총 15번 측정한 뒤 이를 평균 내어 활용하여 자료의 신뢰도를 더욱 향상시킬 수 있다(Minsley et al., 2011). 비분극 전극들은 장기간 동안 상대적으로 안정된 전위 값을 제공할 수 있다는 장점이 있지만, 전해액 보충 등 전극 설치 후에도 관리가 필요하다는 어려움이 있다(Petiau and Dupis, 1980; Corwin and Bulter, 1989; Kang et al., 2014).
안정적인 비분극 전극 사용하는 것뿐만 아니라 민감도가 좋은 전압계를 활용하는 것이 유동전위를 보다 정확하게 측정하기 위해서 중요하다. 민감도가 0.1 mV, 내부(input) 임피던스는 100 Mohm 인 Metrix MX20를 이용하거나, 이와 비슷한 성능의 Fluke 289 전압계(voltmeter)인 M-6000M(METEX)과 같은 별도의 자연전위 탐사기를 사용하여 좋은 결과를 얻은 사례들이 있다(Bolève et al., 2009 & 2011; Wang et al., 2018). 위와 같이 민감도가 좋은 별도의 전압계를 사용하는 것 외에도, 전기비저항 탐사 수행 시 자연전위 탐사를 함께 수행할 수 있다는 장점이 있는 전기비저항 측정 장비인 ABEM 사의 AC Terrameter, SAS-300 DC 와 같은 탐사 기기를 활용하여 자연전위 탐사를 수행하기도 하였다(Song et al., 2000; Dahlin et al., 2001).

3.4. 지전류 모니터링 통한 잡음 분석
누수 탐사 시에는 잡음이 수리 시설물 혹은 호수, 강에서의 수위 변화, 온도 변화와 같은 일변화 등에 의해서 발생할 수 있다. 이러한 잡음의 영향을 고려하기 위해 지전류 모니터링과 같은 배경 탐사를 함께 수행하여 흐름 전위 신호 해석에 신뢰도를 높일 수 있다. 지전류 모니터링을 수행하기 위해서, 육상에서는 저수지 중심 코어 상부에 Cu-CuSO₄ 비분극 전극을 벤토나이트를 포함하는 혼합토(bentonite mix)로 채워진 bag에 넣어 6 m 간격으로 매립하여 2초 간격으로 자연전위를 측정하였다. 해상에서는 50 m 간격의 쌍극자에서 매초 전위를 측정하여 두 자료를 비교하였을 때, 각각 100 m 당 최대 3 mV, 10 mV 차이가 있었다(Dahlin et al., 2001). 한편, Minsley et al. (2011)은 자연전위 측선 중 일부와 거의 일치하는 영역에 대해 비분극 전극을 0.6 m 깊이에 219 m 떨어뜨려 설치하고 MT-24LF 측정 장비를 활용하여 지전류 변화를 측정하였는데, 측정 결과 ft 당 2 μV 정도의 차이만이 나타났다. 두 연구 모두에서 알 수 있듯이(두 연구 사례 모두 배경 전위가 측정된 전위와 비교했을 때 큰 차이가 없어 추가적인 보정은 하지 않았다), 흐름 전위 이상의 크기가 상대적으로 작기 때문에 누수에 의한 영향 외에 발생할 수 있는 다른 영향을 고려하여 해석하는 것이 중요하다.

흐름 전위는 강한 이온 농도 차이 혹은 산화 환원 기울기 등에 의해 수 백 mV의 세기로 발생하는 전기화학적 전위와 비교하여 상대적으로 약한 수 mV에서 수십 mV로 세기로 발생한다. 또한 수두 기울기 방향과 반대로 전위 기울기가 나타나는 특성에 따라 누수로 인한 흐름 전위 이상은 대체로 음 값을 보인다. 그러나 기준 전극의 위치와 측정 전극이 위치하고 있는 영역에서 물의 흐름 방향에 따라 양의 이상이 나타날 수 있는데, 예를 들어 지하수의 상향흐름이 발달한 제체의 하류사면 끝 부분에서 양의 이상이 나타난다(Bolève et al., 2009; Ikard et al., 2014). 흐름 전위 자료에서 공간적으로 이상대 분포를 해석하기 위해서는 각 측점에서의 흐름 전위 자료들을 바탕으로 2D 이미지로 도시하는 것이 효과적이다. 3D 탐사를 수행하여 취득한 흐름 전위 자료를 전극 사이 자료가 없는 영역은 내삽을 통해 전기비저항 이미지처럼 도시하여 유체 흐름 방향 및 누수를 보다 효과적으로 파악할 수 있다(Fig. 4)(Bolève et al., 2009).
누수에 의한 흐름 전위 이상 외에 지하 지질 특성에 의해서도 흐름 전위 이상이 발생할 수 있다. 절리가 발달한 지역에서도 절리를 통한 지하수 흐름에 따라 흐름 전위 이상이 나타나는데, 절리 부근에서의 강한 양의 이상 또는 양과 음의 이상이 섞여 나타나거나(Blèvre and Norgeot, 2005), 기반암 단층 구역으로의 지하수의 수직 하강 흐름으로 약 – 100 mV의 이상이 나타나기도 한다(Moore et al., 2011). 또한 가파른 지형 아래 얕은 심도에서 지하수가 흐를 때 가장 높은 고도에서 가장 작은 이상이 나타나는 현상(negative summit)이 나타나기도 한다(Fig. 5) (Dahlin et al., 2001; Moore et al., 2011). 흐름 전위 송신원은 전기전도도 분포에도 영향을 크게 받기 때문에(7(식)), 공극수의 전기전도도 변화에 따라 흐름 전위도 변화한다(Bolève et al., 2011).
지형 변화 및 절리와 같은 지질 구조에 의한 흐름 전위 이상을 누수 이상으로 해석하지 않기 위해서는, 탐사 지역의 지질 자료를 함께 해석하는 것이 좋다(Blèvre and Norgeot, 2005; Moore et al., 2011; Wang et al., 2018). 배경 지질 자료가 없는 경우에는 대체로 누수에 의한 이상보다 지질 구조에 의한 이상이 상대적으로 크게 나타나므로 누수에 의한 흐름 전위 이상 값으로 적합한지 정성적으로 판단해야 한다. 또한 외부 환경에 변화를 주어 누수 영역에서의 흐름 전위 이상이 변화하도록 하거나 다른 물리 탐사 방법을 함께 수행하여 해석할 수 있다.
흐름 전위 자료는 잡음 및 현장 특성에 따라 영향을 받을 수 있으므로 다양한 탐사 방법 및 참고할 수 있는 기타 지표와 함께 복합 해석하는 것이 누수 유로를 파악하는 데 유리하다. 자연전위 탐사와 함께 가장 많이 수행되는 물리탐사 방법은 전기비저항 탐사이다(Bolève et al., 2012). 전기비저항 탐사는 같은 전극 배열을 활용할 수 있다는 장점 외에도 지하의 전기비저항 구조에 대한 사전 정보를 제공하며 정량적 해석 시 지하의 전기비저항 분포 자료를 제공한다는 점에서 활용도가 높다.
전기비저항 탐사 외에도 수동형 표면파 탐사(Micro- tremor survey)를 통해 지하의 S파 속도 분포를 파악하여 SP 자료와의 복합 해석을 수행할 수도 있다(Wang et al., 2018). 또한 음향 방출(acoustic emission) 혹은 수중 음향(hydro-acoustic) 탄성파 탐사를 자연전위 탐사와 함께 수행하여, 댐 내부의 부식으로 인한 예상 탄성파 소스 발생 지점 분포를 예측하여 흐름 전위 자료 해석을 보다 향상시킬 수 있다(Bolève et al., 2012; Rittger et al., 2015). 댐 상부 및 강 내부에서 전기비저항 탐사 외에도, radio-magnetotelluric 탐사, 탄성파 굴절법, 그리고 GPR 탐사를 적용하여 주변 지질 및 댐 내부 누수 영역을 분석할 수 있다(Bièvre and Norgeot, 2005).

수리시설물에서 측정된 흐름 전위는 정성적 혹은 정량적으로 다양한 자료들과 함께 공간적 혹은 시간적 전위 변화를 해석하여 누수 영역을 복합 해석한다. 정성적으로 흐름 전위를 해석할 때에는 다른 자료와 함께 해석하거나 환경에 인위적인 변화를 주면서 모니터링을 수행하고 이에 따른 흐름 전위 변화를 관측하여 누수 영역을 평가할 수 있다. 정량적 흐름 전위 자료 해석은 지하의 전기적, 수리적 물성을 매질의 특성에 맞게 정의한 뒤, 수리 시뮬레이션을 수행하고 측정 전위와 지하의 전류 밀도의 선형 관계를 이용하여 지하의 전류 밀도 분포를 구함으로써 수행된다. 여기서는 수리시설물에서의 흐름 전위에 대한 정성적 및 정량적 해석 사례에 대해 살펴본다. 특히 정성적인 해석 사례에서는 기타 탐사법과의 비교를 통해 흐름 전위 자료를 해석하는 사례들 외에 흐름 전위 모니터링 자료만을 활용하여 누수를 해석한 사례에 초점을 두었다.

5.1. 정성적 해석 사례들
흐름 전위를 정성적으로 해석하기 위해서는 지질 정보를 포함한 다양한 자료들을 함께 고려하여 해석하는데, 흐름 전위 자료만을 이용해도 효과적으로 누수 영역을 관측할 수 있다(Bulter and Llopis, 1990). 배경 흐름 전위와 지하수위 변화에 따른 흐름 전위를 연속적으로 취득한 뒤 지하수위 변화나 일 변화에 의한 누수 외의 영향에 의한 전위를 제거한 뒤 누수를 평가한 결과, 지하수위가 높아지면서 증가하는 수두로 인해 누수 지점에서 더욱 강한 흐름 전위 신호를 관측할 수 있다. 이를 위해 지하수위 변화 전 흐름 전위 평균 값과 지하수위 변화 이후 흐름 전위 평균 값의 차를 구한 뒤 지하수위 변화 이후 측정한 흐름 전위에서 제거함으로써 지하수위 변화에 의한 영향을 흐름 전위에서 제거하였다. 이러한 흐름 전위 자료에서 각 전극 위치에서의 배경 전위를 제거함으로써 일 변화 및 기타 효과를 제거하여 누수에 의한 흐름 전위 이상만을 관측할 수 있다. 이에 따라, 흐름 전위 모니터링 자료만을 활용하여 잡음 제거 및 누수 영역이 성공적으로 관측되었다(Bulter and Llopis, 1990).
한편 흐름 전위가 유체의 NaCl 농도 증가에 따라 선형적으로 증가한다는 실험 결과에 따라, 지하수의 염도의 변화를 주어 이에 따른 누수 영역에서의 흐름 전위 변화를 관측하여 누수 영역을 평가한 사례가 있다(Fig. 6)(Bolève et al., 2011). 이에 기초하여 댐에서 추적자시험(tracer test)을 위한 소금물 주입 후의 흐름 전위 자료에서 주입 전 배경 흐름 전위 자료를 제거하여 양의 이상이 나타나는 영역을 누수 영역으로 해석하였다. 누수 영역으로 해석된 영역에서의 전기전도도 변화 자료에서도 뚜렷한 전도도 증가가 나타났다. 위와 같이 흐름 전위 해석 시 주위의 환경을 인위적으로 바꾸어 모니터링을 수행하고 이에 따른 전위 변화를 정성적으로 해석함으로써 누수 영역을 효과적으로 평가할 수 있다.
방조제에서도 자연전위 탐사를 수행하여 바닷물이 내륙까지 침투하는 것을 분석한 사례가 있다(Song et al., 2000 and 2002; Kang et al., 2014). 방조제에서의 자연전위는 조석 변화에 따라 변화가 크게 나타나는데, 바닷물의 흐름 방향이 변동함에 따라 전위의 부호도 바뀌게 된다. 방조제에서의 자연전위 탐사는 전기비저항 탐사, 지하수의 전기전도도 및 수온 측정과 함께 수행하여 해석할 수 있다(Song et al., 2000; Kang et al., 2014). 이 때 단극 배열 전기비저항 탐사는 지하 정보가 지나치게 단순화되어 해석에 어려움이 있으며, 자연전위 탐사는 조석 주기를 고려하여 일정 간격으로 탐사를 수행하고 인접 측점 간 전위 변화도 크게 나타나는 점을 고려하여 한 측점에서 시간에 따른 전위 변화 추이를 분석하는 것이 보다 효과적이다(Kang et al., 2014). 지하수 정보와 함께 해석할 때에는 수온이 상대적으로 낮고 전기전도도가 높게 측정되는 지점에서 음의 흐름 전위 이상이 나타났다(Song et al., 2000).
그런데 최근 해안 인근 영역에서 시추공을 이용한 자연전위 자료 분석을 통한 해수 침투를 분석한 연구에서, 해수 침투로 인한 자연전위는 흐름 전위 보다 전기화학적 전위에 의한 영향이 주되게 나타나는 것을 증명하였다(MacAllister et al., 2016). 이 때의 전기화학적 자연전위(exclusion-diffusion potential)는 다공질 매질 내에서 서로 다른 용액이 접촉하여 전해질 농도 차이가 나타남에 따라 발생한다(Westermann-Clark and Christoforou, 1986). 위의 전기화학적 전위에 따라 해수의 영향이 가까워질수록 해안가의 시추공 내에서 측정한 자연전위 값의 변화가 나타남을 보였다(MacAllister et al., 2018). 이에 따라 방조제에서의 해수 침투를 해석하기 위해서는 흐름 전위 뿐만 아니라 전기화학적 전위를 고려하여 해석해야 한다. 또한 방조제에서 자연전위 탐사 수행 시 스테인리스 전극은 해수와의 산화환원 반응이 발생하여 산화환원 전위가 발생할 수 있으므로 주의하여야 한다(MacAllister et al., 2016).

5.2. 정량적 해석 사례들
흐름 전위 자료의 정량적 해석을 위해, 댐에서의 누수 혹은 지질 환경을 모사하여 수치 시뮬레이션을 반복적으로 수행하고 현장 자료와 비교하는 방법(시행착오법)을 이용하거나 탐사 자료의 역산을 수행할 수 있다. 흐름 전위 모델링 및 역산 수행 시 Comsol Multiphysics를 사용하여 정량 해석을 수행한 경우가 많다(Bolève et al., 2009, 2011, and 2012; Moore et al., 2011; Soueid Ahmed et al., 2019). 이러한 수치 시뮬레이션이나 자연전위 탐사 자료의 정량적 역산 등을 통해 흐름 전위를 정량적으로 해석한 사례들을 분석하였다.

5.2.1. 수치 시뮬레이션을 통한 정량적 해석 사례들
누수에 따른 흐름 전위 반응 모델링은 Comsol Multiphysics를 이용하여 누수를 가정한 후, 수치 모델을 구성하고 Darcy 혹은 Richared 식과 포아송 식을 바탕으로 흐름 전위를 계산 가능하다. Richard 식을 사용할 때에 누수 모델은 2D로 댐을 가로지르는 투과도가 좋은 영역을 설정하여 우선적 유동 경로를 구성함으로써 구현하였고, 매질의 물성들(단위 부피당 과전하, 공극률, 수리전도도 등)은 van Genuchten 매개변수들을 활용하여 설정하였다(Bolève et al., 2009). 2D 모델링을 기반으로 3D 모델링도 수행되었는데, 3D 저수지를 구현하고 수위를 높여가며 수위가 증가함에 따라 흐름 전위가 증가함을 정량적으로 분석하였다(Minsley et al., 2011). 이와 같이 탐사 대상을 구현하여 흐름 전위 모델링을 수행함으로써 기준전극을 기준으로 관심 영역 내의 전위 분포를 파악할 수 있는 장점이 있다. 또한 모델링 결과를 취득한 흐름 전위 자료와 비교하며 누수 영역을 해석할 수 있다.
특히 전기 문제에서 포아송 식을 풀 때 지하 전기전도도 분포를 설정해야 한다. 수리시설물 내부 전기비저항은 van Genuchten 매개변수를 활용하거나 시설물 내부의 각 매질의 대표적인 전기비저항 값을 가정하여 설정한다. 특히 댐 내부의 중심 코어와 같은 점토질은 점토의 표면전도도(10^-2 ~ 10^-1 S/m)(Revil and Hermitte, 2002)와 지하수의 전기전도도 비로 정의되는 Dukhin number의 범위에 따라 전기전도도를 계산할 수 있다(Revil et al., 2002; Bolève et al., 2012). 현장을 모사한 수치 모델을 구성할 때에는 현장에서 전기비저항 탐사를 수행하고 취득한 전기비저항 자료를 역해석하여 얻은 전기비저항 분포를 사용할 수 있다.
댐을 구현한 테스트 베드에서 누수에 따른 흐름 전위를 모니터링하고 흐름 전위 반응 모델링을 수행한 연구에서는, 테스트 베드와 실제 누수 영역을 고려하여 수치 모델을 구현하고 누수가 발생하는 영역 근처 실제 흐름 전위 신호 측정 지점에서의 전위 크기를 계산하였다(Soueid and Ahmed et al., 2019). 이 모델링을 통해 높은 레이놀즈 수와 누수 영역의 PVC 관의 영향으로 흐름 전위가 감소하는 것을 관측하였고, 흐름 전위 신호 세기를 키우기 위해 유체 흐름이 점성 층류에 가깝도록(레이놀즈 수의 영향을 줄이고자) 누수 시작 영역에 모래 주머니(sand bag)을 추가하여 흐름 전위 값을 향상시켰다.
국내에서는 Sill(1983)의 연구 결과를 기초로 하는 모델링 알고리듬(Yang, 2001)을 이용하여 서로 다른 누수 특성을 가진 저수지들을 대상으로 2D 수치 모델링을 수행하였다(Song et al., 2002). 수치 모델은 기반암과 댐체, 누수 영역을 나누어 영역 별로 전기비저항, 투수율, 유동 전위 결합계수를 가정하여 구성하였고 현장의 누수지점에서 취득한 누수량을 활용하여 모델링을 수행하여 현장 자료와 유사하게 나타남을 보였다. 이 때 누수 유형과 같은 누수 정보를 바탕으로 모델을 구성한다는 점에서 사전 정보가 없을 때의 해석은 한계가 있다.

5.2.2. 흐름 전위 역산 사례들
흐름 전위 역산 수행 시 실제 수리시설물을 구현하여 모델링을 수행하고 모델링 결과를 역산에서 이전 모델로 사용한다. 또한 지하의 전기비저항 분포를 설정해야 하는데, 전기비저항 분포는 댐 내부의 매질 별 전기비저항 값을 설정하거나 대체로 자연전위 탐사와 동일한 영역에서 수행된 전기비저항 탐사 자료를 역해석하여 취득한다(Bolève et al., 2009 and 2011; Rittgers et al., 2015). 전기비저항 역산 결과를 흐름 전위 역산에 이용하는 경우 전기비저항 역산 결과의 신뢰성에 대한 한계점이 존재한다(Bolève et al., 2009).
제방과 내부 점토 코어로 이루어진 댐을 2D로 구현하고 Comsol Multiphysics 유한요소 코드를 활용하여 흐름 전위를 모델링한 뒤 2D 역산을 수행한 연구에서는, 높은 전류 밀도가 나타나는 예상 누수 영역을 해석할 수 있었다(Bolève et al., 2009). 이를 검증하기 위해 측정된 흐름 전위 자료와 역산 자료를 비교하는 것뿐만 아니라 댐 상부에 시추공을 뚫고 투수율을 평가하기 위한 지반 테스트를 수행한 뒤 비슷한 심도에서 투수율이 높게 나타나는 것을 보임으로써 흐름 전위 역산 결과를 효과적으로 검증하였다.
테스트 베드에서 취득한 흐름 전위 모니터링 자료를 활용하여 음향 방출 탐사와의 복합 역산 및 시간 경과 역산을 수행한 사례도 있는데, 여기서 자연전위 모니터링은 네덜란드의 북동쪽에 위치하고 있는 실물 크기의 댐에서 2007년부터 2012년까지 수행된 파괴 시험(IJKDIJK experi- ment) 중 마지막 시험 시 하였다(Ritters et al., 2015). 일정 기간 동안 취득한 모니터링 자료를 역산 수행 시 추가적인 제한 조건을 주어서 한 번에 역산하는 4D 흐름 전위 역산을 통해 소스 전류 밀도를 직접 계산하였다(Jardani et al., 2008; Kim et al., 2009; Karaoulis et al., 2014). 또한 자연전위 탐사와 함께 수행된 수동적 물리탐사인 음향 방출 탐사 결과도 흐름 전위 역산 시의 계산 영역에 맞추어 외삽하고 이를 스칼라 가중치로 계산하여 평활화 제한조건에 적용함으로써 소스 전류 밀도의 크기를 보정하는 데 사용되었다. 역산 결과 음향 방출 결과와 복합 해석한 흐름 소스 전류 밀도 벡터장이 보다 현실적인 유체 흐름을 보여주며 누수 부근 흐름 전위 이상이 보다 잘 집중되어 나타나 흐름 전위의 정량적 해석에서의 복합 해석 가능성을 잘 보여주었다.
5.2.3. 흐름 전위 역산 결과를 이용한 수리 상수 평가
흐름 전위 역산 수행 시 취득한 역산 결과를 바탕으로 누수 속도나 투수율을 평가하는 연구도 수행되었다(Bolève et al., 2009 and 2012; Ahmed et al., 2020). 이는 다양한 매질에 대해서 실험을 수행하여 투수율, k(m²)과 단위 공극 부피당 과전하, Q̅_v[C/m³] 각각의 로그 값들과의 관계를 정리한 아래의 경험식을 바탕으로 한다.



여기서 a와 b는 각각 9.9956, 0.9022이며, 이 값은 Bolève et al. (2012)이 보다 넓은 범위의 투수율 분포를 고려할 수 있도록 보완한 결과이다(Fig. 7). 위의 식을 바탕으로, 댐에서 측정한 수리전도도 값을 기반으로 투수율과 이에 따른 Q̅_v를 계산하고 식(9)를 바탕으로 흐름 전위 역산 결과로부터 누수 속도를 추정할 수 있다(Bolève et al., 2009).
Bolève et al. (2012)는 수중 음향 측정 자료를 바탕으로 누수 영역(표면적)을 가정하고 수리 기울기를 일정 값으로 고정하였을 때 누수 영역에서의 흐름 전위와 전기비저항을 바탕으로 투수율을 평가하고자 하였다. 레이놀즈 수를 고려하여 레이놀즈 수를 무시할 수 없는 높은 투수율 범위에서도 적용할 수 있도록 하였다. 위와 같이 흐름 전위 역산 결과를 바탕으로 누수 속도 및 투수율을 평가하기 위해서는 제한된 모델을 설정하고 실험식에 의존한다는 점에서 정확도의 한계가 있지만 흐름 전위 역산 결과로부터 투수율을 평가하는 기초 연구로서 의의가 있다.

수리시설물에서의 자연전위 탐사는 주된 유체 흐름이 있는 누수 영역을 해석하고 외부 송신원 없이 지속적인 모니터링이 가능하다는 점에서 큰 장점이 있다. 그러나 자연전위 신호의 세기가 작고 이에 따른 잡음의 영향이 크며 정량적 해석에 한계가 있어 자연전위 탐사 적용에 어려움이 있다. 이에 따라 국내외의 여러 사례에서 잡음의 영향을 최대한 줄이고 누수를 평가하기 위한 연구들이 많이 수행되었으며, 누수를 효과적으로 해석하기 위해 다른 탐사 방법들과 복합 해석을 하거나 현장 지질 특성을 고려하여 정성적 및 정량적 해석을 수행하였다. 흐름 전위 자료만으로도 탐사 시에 염도나 지하수위 변화와 같은 외부 환경 변화를 발생시켜 누수에 의한 흐름 전위 반응을 보다 뚜렷하게 함으로써 누수를 성공적으로 평가하였다. 특히 최근 자연전위 자료를 정량적으로 해석하는 연구들이 늘어나면서 시간 경과 및 기타 탐사 자료와의 복합 해석을 통해 누수를 평가하였다. 또한 정량적 해석 결과로부터 누수 영역에서의 수리 상수 평가도 수행되며 자연전위 탐사의 활용도가 높아지고 있다. 수리시설물에서의 여러 사례들을 분석하며 수리시설물 내부의 복잡한 수리 환경 및 전기적 분포의 불확실성 등의 누수 평가의 한계들이 있지만 주변 환경을 고려한 정성적 해석 및 다른 탐사 혹은 시추공 자료와의 복합 해석을 통한 정량적 해석을 수행한다면 보다 효과적으로 누수를 평가할 수 있을 것으로 기대된다.

이 연구는 2021년도 원자력안전위원회의 재원으로 사용후핵연료관리핵심기술개발사업단 및 한국원자력안전재단의 지원을 받아 수행된 연구사업(No. 2109092-0121-WT112)과 산업통상자 원부의 재원으로 KETEP의 지원을 받은 연구 과제입니다(No. 20194010201920).