In order to properly evaluate the spatio-temporal variations of groundwater flow, the data obtained in field experiments should be corroborated into numerical simulations. Particle tracking method is a simple simulation tool often employed in groundwater simulation to predict groundwater flow paths or solute transport paths. Particle tracking simulations visually show overall the particle flow path along the entire aquifer, but no previous simulation studies has yet described the parameter values at grid nodes around the particle path. Therefore, in this study, a new technical approach was proposed that enables acquisition of parameters associated with particle transport in grid nodes distributed in the center of the particle path in groundwater. Since the particle tracking path is commonly referred to as streamline, the algorithm and codes developed in this works designated streamline analysis method. The streamline analysis method can be applied in two-dimensional and three-dimensional finite element or finite difference grid networks, and can be utilized not only in the groundwater field but also in all fields that perform numerical modeling.

Keywords: groundwater modeling, particle tracking, streamline, streamline analysis method

지하수 유동 모델은 지하수 수위를 평가하거나 양수정과 같은 스트레스에 대한 대수층 반응을 평가하는데 사용될 뿐만 아니라, 흐름 경로를 평가하거나 지하수 내 용질의 이송 및 분산을 평가하기 위한 배경값으로도 사용된다. 입자 추적(particle tracking)은 이러한 흐름 경로나 용질의 이송 경로를 간단히 평가하기 위해 지하수 유동 모델과 함께 사용되는 기법의 하나이며, 주요 장점 중의 하나는 순방향뿐만 아니라 역방향 추적이 가능하다는 점이다.
Maskey et al.(2002)은 입자 추적 기법을 사용하여 오염운 제거를 위한 양수율과 양수정 위치 결정을 위한 최적화 알고리즘을 제시하였으며, Yidana(2011)는 가나의 일부 대수층에서 함양의 흐름 경로를 정의하기 위해 입자 추적 기법을 사용하고, 흐름 경로를 따라 함양지에서 배출지까지 이동 시간을 규명하였다. Stollberg(2013)는 독일 Bitterfeld-Wolfen Megasite에서 오염물질이 산출된 관측정을 기준으로 입자 역추적 모의를 실시하여 오염원의 발생지점을 역추적하였으며, Thakur(2013)는 Bitterfeld-Wolfen 지역의 지하수 관측망 최적화를 평가하기 위해 입자추적을 수행하고 동일 경로상에 위치하는 관측정 중 필수 관측정을 선택할 것을 제시한 바 있다. Klaas et al.(2017)은 카르스트 대수층에서 입자 추적 기법을 사용하여 지하수 취약 구역을 생성하였으며, Alberti et al.(2018)은 몬테카를로 입자 추적 기법을 사용하여 지하수에서 테트라클로로에틸렌을 평가하고 확산 영역을 식별하였다. 국내에서는 일반적으로 MODFLOW(Harbaugh, 2005)와 MODPATH(Pollock, 1994)가 많이 알려지고 활용되고 있다. Hamm et al.(2005)은 창원시 낙동강 하안의 강변여과수 취수장에 대한 지하수 모델링을 바탕으로 물수지 분석과 함께 입자 추적을 실시하여 취수정의 영향을 분석한 바 있으며, Kwon(2005)은 폐기물매립장의 침출수 거동 현상을 모의하고, 채수에 따른 포획구간 및 유동 경로 분석을 위해 입자 추적 모의를 시행하였다. 중저준위 방사성 폐기물 처분장의 건설 및 운영으로 인해 처분장 부지에서의 지하수 유동 연구 및 예측의 중요성이 높아짐에 따라, Ko et al.(2012)은 한국원자력연구원의 지하처분연구시설인 KURT 부지에 대한 지하수 유동을 모의하고, 국지 규모에서의 입자 추적을 수행하여 가상의 심층 처분시설에서 지표로 향하는 유동 경로를 확인한 바 있으며, Kim(2019)은 방사성 폐기물 처분장에 대한 안전성 평가의 하나인 우물 시나리오에 관한 연구에서 FEFLOW (Diersch, 2014)를 이용한 지하수 유동과 입자 추적 모의를 수행하여 처분장에서부터 우물로 유입되는 입자의 비율을 계산하였다.
최근에는 국내 원자력발전소의 운영 기간이 늘어남에 따라 고준위 방사성 폐기물 처분에 관한 관심이 높아지고 있다. 이미 운용 중인 중저준위 방사성 폐기물 처분장뿐만 아니라 앞으로 건설이 계획되어 있는 고준위 방사성 폐기물 처분장의 부지 선정, 건설 중, 건설 후 운영 중, 폐쇄 후 각각의 단계별로 안전성 평가가 수행되어야 한다. 예를 들면, 운영 중 또는 폐쇄 후 처분장 기능이 상실되는 경우, 방사성 폐기물에 함유된 핵종이 지하수 유동을 통해 다양한 경로로 이동되어 생태계에 방사선적 영향을 미칠 수 있게 된다. 안전성 평가에서는 이와 같은 다양한 가상의 시나리오를 바탕으로 방사선적 영향을 평가하게 되며, 이때 이동 경로뿐만 아니라 경로의 길이 및 경로의 비유량 또는 Darcy 유속이 평가를 위한 입력자료로 필요하다. 핵종의 이동 경로는 입자 추적 모의를 통해 규명되는데, 지금까지의 입자 추적 모의는 추적 결과를 시각적으로 도시하는 수준이며, 경로에 따른 Darcy 평균유속을 직접적으로 산정할 수는 없다. 입자 추적 모의를 통해서도 경로별 경과시간이 산출되지만, 이는 유효공극율이 반영된 시간으로, 모델의 입력값으로 유효공극율이 변화되면, 입자의 이동 속도도 바뀌게 된다. 즉, 경로에 따른 입자의 평균 이동 속도는 유효공극율에 따른 불확실성을 내포하고 있다. 따라서 경로에 따른 Darcy 평균유속은 입자 추적 경로 주변의 지하수 유동 모의 결과로부터 평가되어야 한다.
본 연구에서는 격자망 내부에서 모의된 입자 경로를 활용하여, 경로를 중심으로 일정한 범위 안에 포함되는 주변 격자점에서의 정보를 취득하는 기술을 개발하고자 한다. 입자 추적경로를 유선(streamline)이라고도 하므로, 본 연구에서 개발하는 알고리즘 및 수치모형을 유선 분석법(streamline analysis method)이라고 명명한다. 개발된 알고리즘을 코드화한 후, 기존 수치모의 결과에 개발된 유선 분석법을 적용하여 결과를 산출하고, 활용법에 대해서 토의하고자 한다.

2.1. 알고리즘 개발
하나의 유선을 발생시켰을 때, 유선 경로를 따라 절점(node) 및 정점(vertex) 각각에서의 공간좌표 및 경과시간을 획득할 수 있다. 여기서, 유선은 연속선(polyline)과 같으며, 따라서 절점은 연속선의 시작점과 끝점을 나타내고, 정점은 연속선의 중간점을 지시한다. Fig. 1은 연속선의 시작부분을 나타내고 있는데, S1은 유선 즉 연속선의 시작 절점이며, S2는 유선의 정점을 나타낸다. P1~P3는 3차원 모델 격자망에서의 격자점(grid points)에 해당하며, S1에서 시작하여 S2를 거쳐 뻗어나가는 직선이 유선을 나타내고 있다. S1과 S2 사이를 연결하는 직선 형태의 선분 S12에 포함되는 격자점을 평가하기 위해서 선분을 반경 r의 원통으로 가정하면, Fig. 1과 같이 격자점 P2는 원통에 포함되지만, P1과 P3는 원통 바깥에 위치하므로 제외되어야 한다.
원통 내부에 격자점이 포함되는지를 평가하기 위해서는 우선 원통 축과 격자점 사이의 거리(d)가 원통 반지름(r)보다 작거나 같아야 한다. 원통 축과 격자점 사이의 거리를 계산하기 위해서 공간벡터의 외적 크기를 활용할 수 있다(Fig. 2). 선분 S12의 시작점 S1에서 S2를 향하는 벡터를 v라고 하고, 선분의 시작점 S1에서의 임의의 격자점(Fig. 2에서는 격자점 P1)에 이르는 벡터를 u라고 하면, 벡터 u와 v가 이루는 평행사변형의 넓이는 다음과 같다.



따라서 원통 축에서부터 임의의 격자점까지의 거리는 평행사변형의 높이와 같으며, 아래와 같이 계산될 수 있다.



d≤r이면, 임의의 격자점은 원통 내부에 포함될 가능성이 있게 된다. Fig. 2에서 P1은 확실히 제외되며, P2와 P3는 원통 중심축과의 거리가 원통 반경보다 짧아 원통 내부에 포함되는 조건을 만족한다. 하지만 P3는 해당 원통의 바깥에 위치하므로, P3를 제외시키는 추가적인 조건이 요구된다. 즉, 원통 축과의 수직거리가 원통의 반경보다 작거나 같지만, 해당 원통의 내부에 있는지를 판별해야 하며, 이를 위해 다음과 같은 정사영(orthogonal projection)을 활용할 수 있다.



Fig. 3에서와 같이, S1에서 P3에 이르는 벡터 u의 원통 축 방향으로의 정사영을 계산하면, 원통 축 상에서의 벡터 u의 그림자 길이(p₀)를 얻을 수 있다. 그림자 길이가 원통 축의 길이, 즉 선분 S12의 길이보다 크거나 음의 값이 나오면, 해당 격자점은 원통 내부에 위치하지 않음을 지시한다. 즉, 0≤p₀≤|v|의 조건을 만족하면, 원통 내부에 위치하는 격자점이 된다. 다시 정리하면, 원통 축과의 거리가 원통의 반경보다 작거나 같고, 정사영 값이 원통 길이보다 작거나 같은 양수일 때, 임의의 격자점은 원통 내부에 존재하게 된다.
하지만, 유선의 선분을 원통으로 가정함으로써, Fig. 4(a)와 같이 선분이 변화되는 위치에서 원통 사이의 틈이 발생할 수 있고, 틈에 위치할 수 있는 격자점을 평가할 수 있어야 한다. 따라서, Fig. 4(b)와 같이 유선의 정점 위치를 중심으로 하는 구를 설정한 후, 구 내부에 임의의 격자점이 위치하는지를 평가하게 된다.



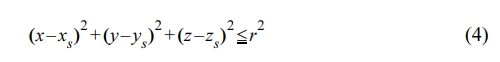
여기서, (x, y, z)는 임의의 격자점 좌표를 나타내고, (x_s, y_s, z_s)는 유선의 정점 좌표를 나타내며, r은 구의 반지름으로 원통의 반경과 동일한 값이다. 원통 사이의 틈에 위치하는 임의의 격자점이 Eq. (4)를 만족하면 유선에 포함되는 격자점으로 평가된다.
2.2. 프로그램 작성
Fig. 5는 유선 분석법에 대한 흐름도를 나타내고 있다. 프로그램을 구동하면 일단 입력값이 요구되는데, 수치 모형을 구성하는 모든 격자점 정보와 모의된 유선 정보 및 유선을 원통으로 가정했을 때의 반경이 입력자료에 해당한다. 공간좌표와 격자점 번호, 그리고 해당 격자점에서 평가된 Darcy 유속값이 격자점 정보에 해당한다. 유선 정보로는 절점 및 정점의 공간좌표와 경과시간이 요구된다. 입력이 완료되면, 모든 유선의 길이와 속력을 평가하게 된다. 모든 격자점에 대해서 유선마다 평가를 반복하는 것은 비효율적이므로, 유선이 존재하는 소규모 직사각형 영역에만 포함되는 격자점을 분리한 후, 주어진 반경의 원통 내부에 위치하는 격자점 정보를 상술한 알고리즘을 이용하여 추출하게 된다. 원통 내부에 위치하는 모든 격자점 정보를 평가하여 결과를 출력한 후, 프로그램은 종료된다.

상술한 알고리즘을 바탕으로 프로그램 코딩을 완료하였으며, 212만 개의 격자점으로 구성된 기존의 FEFLOW 모델링 결과에 개발된 유선 분석법을 적용하였다. FEFLOW 모델링 지역과 수치 모델에 대한 상세한 내용은 Kim(2019)을 참고할 수 있다.
3.1. 원통 반경에 따른 결과
원통 반경 설정에 따른 평가 결과 변화를 살펴보기 위해서, 모의 영역 내 임의의 위치에 유선 발생을 위한 한 개의 입자(seed)를 설정하였다. 발생된 유선의 반경을 각각 5 m, 10 m, 20 m로 설정하였을 때, 유선 원통 내부에 위치하는 격자점의 변화는 Fig. 6과 같다. 그림에서 빨간색 선은 유선을 나타내고, 노란색 점은 유선에 포획된 격자점을 나타내고 있으며, 유선의 반경을 확대할수록 유선 내부에 포획되는 격자점이 증가함을 알 수 있다. 발생된 유선의 길이는 672.201 m이며, 유선의 위치와 경과시간을 이용한 유선의 평균 유속은 7.789×10^-2 m/day이다. 그 밖의 유선 반경에 따른 평가 결과는 Table 1과 같다. 원통 반경이 증가함에 따라 유선이 차지하는 소규모 직사각형 영역의 격자점 개수도 함께 증가하는 이유는 설정한 원통 반경만큼 유선이 차지하는 소규모 영역의 범위를 증가시키기 때문이다.
3.2. 다중 유선 평가
Fig. 7은 261개 입자(그림에서 노란색 점)를 설정하였을 때 총 234개의 다중 유선(그림에서 빨간색 선)이 모의된 결과를 보인다. 총 212만 개의 격자점 중에서 Fig. 7과 같은 다중 유선이 차지하는 소규모 영역에 포함되는 격자점 개수는 142,618개이다. 모의된 총 234개의 유선 중에는 발생 직후에 소멸하는 유선도 존재하게 되며, 따라서 유선의 최소 길이를 설정하여 그 이하의 길이를 갖는 유선은 평가에서 제외할 필요가 있다. 본 사례에서는 1.0 m를 최소 유선 길이로 설정하였으며, 그 결과 234개 유선 중 118개의 유선만이 평가 대상으로 선정되었다. Table 2는 118개 유선을 평가한 결과이다. 118개의 유선 각각에 포획되는 격자점은 유선마다 다르므로, 길이와 유속에 대한 118개의 값을 얻을 수 있고, 따라서 최소, 최대, 평균, 표준편차 값을 산정할 수 있다.
또한, Fig. 7과 같이 118개의 유선이 공간의 일정한 영역을 차지하는 것으로 볼 수 있으므로, 118개 유선에 포획되는 격자점을 모두 모으면 8,564개가 된다. 이러한 8,564개 격자점에서 Darcy 유속의 평균값은 2.746×10^-4 m/day로 평가되며, 본 연구에서는 이를 Darcy 벌크 유속(bulk velocity)이라고 명명한다.
3.3. 우물 포획 평가
Fig. 8은 261개 입자(그림에서 노란색 점)를 설정하였을 때 총 234개의 다중 유선(그림에서 빨간색 선)이 모의된 결과를 보인다. Fig. 8과 같이 영역 내에 양수정(그림에서 자주색)이 존재하는 경우, 양수량에 따라 우물로 포획되는 유선이 존재할 수 있다. 따라서 양수정 효과를 평가하기 위해서, 우물에 포획되는 유선만을 분석할 필요가 있다. 이를 위해 양수정 위치를 중심으로, 설정 반경 내에 들어오는 유선을 우물에 포획된 유선으로 가정하였다. 최소 1.0 m 이상의 유선 길이를 보이고, 우물에 포획되는 유선만을 선택한 결과, 234개 유선 중 86개의 유선만이 평가 대상으로 선정되었으며, 이는 36.752%(=86/234×100)의 포획률에 해당한다. 총 212만 개의 격자점 중에서 우물 포획 다중 유선이 차지하는 소규모 영역에 포함되는 격자점 개수는 25,835개이며, Table 3은 86개 유선에 대한 평가 결과를 나타낸다. 우물 포획 유선에 포함되는 벌크 격자점 개수는 2,767개이며, Darcy 벌크 유속은 1.176×10^-3 m/day이다.

본 연구에서는 3차원 격자망에서 입자 추적경로 또는 유선을 따라 격자점의 정보를 추출하는 기법에 대한 알고리즘을 개발하고 코드화하였으며, 이를 유선 분석법이라고 명명하였다. 기존 유한요소 모의 결과에 적용한 결과, 경로별 위치와 경과시간으로 계산한 유선의 속력과 유선 주변의 격자점에서 추출한 Darcy 유속은 상당한 차이를 보이고 있는바, 이는 입자 추적 경로 모의시 유효공극률이 매개변수로 사용되어 상대적으로 빠른 유선 속력이 계산되기 때문이다. 따라서 유효공극률에 대한 불확실성을 내포하고 있는 유선 속력보다는, 지하수 유동 모의로 도출되는 Darcy 유속을 이용하여 안정성 평가 등에 활용하기를 기대한다. 예를 들어, 지하터널을 설계하고 건설할 때 지하터널의 경로를 따라 본 연구에서 개발한 유선 분석법을 적용하면, 터널 경로에 따른 단위 면적당 유량 즉 플럭스를 평가할 수 있다. 또한, 본 연구에서는 우물로 포획되는 순방향 유선의 평가에 유선 분석법을 적용하였지만, 이와 유사하게 기여도 평가에도 활용 가능하다. 예를 들어, 하천이나 우물 등 여러 지역에서 오염이 발견되었을 때, 오염 관측 지점에 입자를 설정하고 역방향 추적 모의를 수행한 후, 오염원으로 예상되는 지역으로 수렴되는 유선의 비율을 따져 오염 기여도를 평가할 수 있다.
본 연구를 통해 개발된 유선 분석법은 3차원 유한요소 격자뿐만 아니라 유한차분 격자에서도 활용 가능하며, 3차원뿐만 아니라 2차원 모의 영역에서도 활용할 수 있다. 수만 개에서 수백만 개에 이르는 대규모 격자망에서 경로를 따른 격자 정보를 추출하는 본 기법은 지하수 분야뿐만 아니라 수치모델링을 수행하는 모든 분야에서 활용 가능하다. 또한 캐드나 GIS를 활용하여 절점 정보를 추출하는 수동적인 방법에 비해서 계산 속도와 정확도 측면에서 월등하다.

본 연구는 환경부 “지중환경오염·위해관리기술개발사업; 2021002440002”으로 지원받은 과제입니다.