- Hydrological Assessment of Baseflow and Influencing Watershed Characteristics in the Yeongsan and Seomjin Watersheds
Jin Chul Joo1 , Dong Hwi Lee2 , Kyung In Chae1 , Su Ryeon Kim3 , Kangwei Shi3 , Kwang Wook Jung1 , and In Kyun Jung1*
1 Department of Civil and Environmental Engineering, Hanbat National University
2 Water & Environment Co., Ltd.
3 Department of Environmental Engineering, Hanbat National University- 영산강ㆍ섬진강 유역 기저유출 평가 및 유역 특성과 기저유출의 상관성 검토
주진철1 ㆍ이동휘2 ㆍ채경인1 ㆍ김수련3 ㆍShi Kangwei3 ㆍ정광욱2 ㆍ정인균2*
1 국립한밭대학교 건설환경공학과
2 (주)물과환경
3 국립한밭대학교 환경공학과This article is an open access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
This study evaluated the applicability and reliability of various baseflow separation methods in the Yeongsan and Seomjin watersheds, and investigated the relationship between watershed characteristics and the baseflow index (BFI). Both graphical approaches (HYSEP-FIM, SIM, LMM, UKIH-Min, PART) and digital filter methods (Lyne-Hollick 1·2-Pass, Chapman, CM, Eckhardt, EWMA) were applied to estimate BFI, and their performance was assessed using statistical indicators including NSE, KGE, PBIAS, and RSR. Sensitivity analysis revealed that BFI results were highly dependent on parameter settings, particularly for digital filters, with the Eckhardt method demonstrating the most stable and reliable performance, thus identified as the optimal method. Correlation analyses between watershed characteristics (e.g., area, elevation, slope, land use) and BFI showed statistically significant relationships in some main river reaches, while tributary basins exhibited complex interactions requiring multivariate analysis. These findings provide a methodological foundation for future baseflow estimation, and serve as essential baseline data for watershed-scale hydrologic modeling, ecological flow assessment, and integrated water resources planning.
Keywords: Baseflow, Baseflow index (BFI), Digital filter, Graphical method, Parameter sensitivity, Watershed characteristics.
우리나라의 경우 연 강수량의 약 60-70%가 여름철 한두 달 사이에 집중되는 계절적 특성을 지니며, 이로 인해 여름철 홍수기를 제외한 나머지 평수기와 갈수기 동안 하천유량은 대부분 기저유출(baseflow)에 의존하게 된다. 따라서 기저유출은 하천의 수문적, 생태적 기능 유지에 매우 중요한 요소로 작용한다. 하천유량은 일반적으로 직접유출(direct runoff)과 기저유출로 구분되며, 기저유출은 강우 이후 지하수 흐름을 통해 시간이 지나면서 지속적으로 하천으로 유입되는 유량이다. 특히 갈수기 동안 기저유출은 하천유량의 대부분을 차지하며, 수온 조절, 영양염류 희석, 안정적인 흐름 유지 등을 통해 수질과 수생태계 건강성 확보에 핵심적인 역할을 수행한다(Gou and Miller, 2014; Chang et al., 2017). 또한 기저유출은 지하수와 지표수를 연결하는 혼합대(hyporheic zone)를 통해 물리적·화학적 상호작용을 매개함으로써, 지표수-지하수 연계에 기반한 유역 물관리 측면에서도 중요한 개념이다. 이는 특히 기후변화로 인한 유량 변동성 확대와 수자원 불균형이 심화되는 현시점에서 지속가능한 하천유량 관리를 위해 기저유출을 정량화하고 이해하는 것이 필수적임을 의미한다.
기저유출은 하천 유량 중 지하수로부터 기원한 구성 요소로, 통상적으로 동위원소 또는 화학적 추적자를 이용한 방법으로 정량화가 가능하다. 그러나 이러한 방법은 장기간의 현장 측정 시 많은 인력과 비용이 소요되며, 고도의 분석 기술을 요한다는 점에서 실제 적용에 한계가 있다. 이에 따라, 유량 관측 자료를 기반으로 한 비추적 기반 방법들이 널리 활용되고 있으며, 대표적으로 도식적 방법(graphical method), 디지털 필터 방법(digital filter method), 그리고 전도도 물질수지법(conductivity mass balance method, CMB)이 있다. 이 중 디지털 필터 방법은 자동화와 반복성이 우수하여 기저유출 분석에 폭넓게 적용되고 있다(Nathan and McMahon, 1990; Eckhardt, 2005).
국내에서는 다양한 기저유출 분리 기법이 적용되어 왔으며, 하천의 수문학적 특성과 계절성, 토지이용 변화에 따른 기저유출 변동성을 분석하기 위한 연구가 활발히 이루어지고 있다. 예를 들어, Choi et al.(2014)는 4대강 유역의 장기 유량자료를 바탕으로 계절별 기저유출 기여도를 정량화하였고, Lee et al.(2017)은 도식적 방법과 디지털 필터 방법을 비교하여 기저유출지수(baseflow index, BFI)의 시기별 변동성을 평가하였다. Kang et al.(2019)은 전국 유량관측지점의 유량자료를 대상으로 USGS(United States Geological Survey)의 PART(baseflow analysis with recursive techniques) 방법을 적용하여, 도시화 및 토지이용 변화가 BFI에 미치는 영향을 분석하였다. 또한, Kang et al.(2022)은 낙동강 유역 내 지류 하천을 대상으로 도식적 및 디지털 필터 기반의 기저유출 분리기법을 비교·적용하여 각 기법의 적합성과 계절적 안정성 등을 평가하였다. 한편, 전도도 물질수지법(conductivity mass balance, CMB)은 전기전도도(electrical conductivity, EC)의 시공간적 변화만을 활용하여 기저유출을 추정하는 간접 추정기법으로, 상대적으로 비용이 적고 장기 관측이 용이한 장점이 있다. 그러나 국내에서는 전도도 자료의 부족으로 인해 적용 사례가 많지 않으며, Yang(2006)은 전라남도 곡성천을 대상으로 CMB 방법을 실증 적용한 사례를 보고한 바 있다.
국외에서는 USGS에서 개발한 Groundwater Toolbox를 통해 도식적 방법(HYSEP: Fixed Interval Method, Sliding Interval Method, Local Minimum Method) 및 디지털 필터 방법(Lyne-Hollick, Chapman, Chapman-Maxwell, Eckhardt, EWMA) 모두를 적용할 수 있다. 이러한 기저유출 분리 결과의 성능 평가는 통계적 적합도 지표를 통해 수행되며, 일반적으로 사용되는 지표로는 NSE (Nash–Sutcliffe Efficiency), RSR (RMSE–Standard Deviation Ratio), PBIAS (Percent Bias), 그리고 KGE (Kling–Gupta Efficiency) 등이 있다. 국내 연구에서는 대체로 NSE 지표를 기반으로 평가하는 경우가 많지만, 국외 연구에서는 KGE와 같은 종합 지표를 함께 활용하여 모델의 상관성, 분산, 편향을 동시에 고려하고 있다(Gupta et al., 2009).
Xie et al.(2020)는 미국 전역의 2,075개 유역 중 1,815개 유역을 대상으로 도식적 방법인 HYSEP(FIM, SIM, LMM), PART, 디지털 필터 방법인 Lyne-Hollick, Chapman, Chapman-Maxwell, Eckhardt, EWMA의 총 9개 방법으로 기저유출을 분리하였으며, 이를 기반으로 명확한 기준(strict baseflow criterion)에 따라 참값을 설정하였다. 이 연구는 NSE 및 KGE를 활용하여 분리 기법의 성능을 평가하였으며, 그 결과 Eckhardt 방법이 1,145개 유역에서 가장 우수한 성능을 나타낸 반면, Lyne-Hollick 방법은 상대적으로 낮은 성능을 보였다. 또한 BFI와 유역 특성(예: 경사, 토양, 강수 등) 간에는 통계적으로 유의한 상관성이 없음을 보고하였다.
본 연구의 대상인 영산강·섬진강 유역은 타 유역에 비해 농업 면적이 넓고 지하수 이용률이 높은 지역으로, 갈수기에는 지하수가 하천으로 유입되어 하천 유량 및 수질에 중요한 영향을 미친다. 그러나 이 지역에 대한 지하수 기여량의 정량적 분석과 기저유출량 평가는 타 유역(예: 한강, 낙동강 등)에 비해 상대적으로 미흡한 수준에 머물고 있다(Kim et al., 2020). 따라서 영산강·섬진강 유역의 건강한 수생태계 유지와 지속 가능한 지하수 기반 하천 유량 관리를 위해서는 기저유출량을 정량화할 수 있는 적절한 분리 기법과 지표수-지하수 통합 모델링의 도입이 시급하다.
이에 본 연구에서는 기저유출 영향 분석 및 정량화 방안을 도출하고자, 영산강·섬진강 유역의 유량 관측망 데이터를 수집·검토하고, 기저유출 분리가 가능한 관측 지점을 선정하였다. 이후, 기존 문헌에서 제시된 도식적 방법과 디지털 필터 방법을 활용하여 기저유출 분리를 수행하고, 그 결과를 계절별·연간 BFI 분석 및 유역 특성과의 상관성 검토를 통해 종합적으로 평가하였다. 이를 통해 본 연구는 영산강·섬진강 유역에 적용 가능한 최적의 기저유출 분리 방법을 제안함과 동시에, BFI와 유역특성 간 관계를 정량화하여 기저유출에 영향을 미치는 주요 환경인자를 도출하는 것을 목표로 한다.
기저유출지수(baseflow index, BFI)는 전체 하천 유출량(Qtotal)중 기저유출(Qbaseflow)이 차지하는 비율을 나타내는 무차원 수문지표로, 하천 유량에서 지하수 유입의 상대적 기여도를 정량화하는 데 활용된다.

BFI는 유역의 지질, 토양 특성, 지하수위, 강우 분포 등의 수문학적 요소에 따라 달라지며, 연간, 계절별, 월별로 산정이 가능하다. 일반적으로 중위도 지역에서는 겨울철에 지하수 유입이 증가하면서 BFI가 높고, 여름철에는 강우에 따른 직접 유출이 증가하여 BFI가 낮아지는 경향을 보인다(Park et al., 2019). 기저유출량은 동위원소 또는 화학적 추적자를 활용한 추적기반 방법(tracer-based method)을 통해 정밀하게 산정할 수 있지만, 장기간 적용을 위한 인력, 비용, 기술적 제약이 크기 때문에, 전통적으로는 유량 자료를 기반으로 한 비추적 기반 분리법(non-tracer-based method)이 널리 활용되고 있다. 이러한 방법은 수문곡선을 기저유출(baseflow)과 직접유출(direct runoff)로 구분하는 이원성 개념에 기반하며, 주요한 비추적 기반 분리 방법에는 도식적 방법(graphical method), 디지털 필터 방법(digital filter method), 전도도 물질수지법(conductivity mass balance method, CMB) 등이 포함된다(Nathan and McMahon, 1990; Eckhardt, 2005; Kang et al., 2022).
2.1.도식적 방법(graphical method)
도식적 방법은 가장 전통적인 기저유출 분리 기법 중 하나로, 대표적으로 지하수 감수곡선법(recession curve method), 수평 직선 분리법(horizontal line method), N-day 최소유량 연결법(N-day minimum method), 가변 경사법(variable slope method) 등이 있다(Kang et al., 2021). 이러한 방법들은 주로 USGS의 HYSEP(Sloto and Crouse, 1996), PART(Rutledge, 1998), 그리고 UKIH(United Kingdom Institute of Hydrology)(Piggott et al., 2005) 등에서 구현되었다. HYSEP 프로그램은 세 가지 방법, 즉 FIM(Fixed-Interval Method), SIM(Sliding-Interval Method), LMM(Local Minimum Method)으로 구성되어 있으며, 각 방법은 유량곡선의 저점값 탐색 기준과 간격에 따라 차이를 보인다. 도식적 방법은 수문곡선에서 특정 지점을 연결하거나 국지적 최소값을 이용하여 기저유출 곡선을 구성하므로, 기저유출의 시간에 따른 점진적 변화를 충분히 반영하지 못하는 단점이 있다. 그럼에도 불구하고 PART 방법은 간단한 적용성과 비교적 우수한 추정 성능으로 인해 일부 연구에서 높은 평가를 받고 있다(Xie et al., 2020).
2.2.디지털 필터 방법(digital filter method)
디지털 필터 기반 기저유출 분리 방법은 하천 유출 시계열을 주파수 관점에서 분해하여, 강우에 즉각 반응하는 고주파 성분은 지표유출(direct runoff)로, 점진적으로 반응하는 저주파 성분은 기저유출(baseflow)로 간주하는 방식이다(Nathan and McMahon, 1990). Lyne-Hollick(1979)은 이러한 개념을 적용한 최초의 필터링 알고리즘을 제안하였으며, 이후 Chapman(1991), Chapman과 Maxwell(1996), Eckhardt(2005), EWMA(Tularam and Ilahee, 2008) 등의 다양한 방식이 개발되었다. 이들 방법은 필터 횟수(pass)와 감수상수 계수(α 등)의 설정에 따라 분리 결과가 달라지므로, 매개변수 설정의 정합성이 중요하다(Ladson et al., 2013). 이 중 Eckhardt(2005) 방법은 지하수 감수계수 α와 기저유출 최대 비율 BFImax 두 가지 매개변수를 활용하여 지하수 기여를 반영할 수 있는 보편성이 높고, 다양한 유역에서 우수한 성능을 보여 널리 활용되고 있다(Eckhardt, 2005; 2012). 실제 다수의 비교 연구에서는 Lyne-Hollick, Chapman, Chapman-Maxwell, EWMA보다 Eckhardt 필터가 더 높은 적합도와 일관성을 보이는 것으로 보고되었다(Xie et al., 2020). (Table 1)에 Lyne-Hollick, Chapman, Chapman-Maxwell, Eckhard, EWMA 방법에 활용한 식과 주요 매개변수를 제시하였다.
2.3.전도도 물질수지법(CMB, conductivity mass balance method)
하천유출에서 기저유출을 분리하는 방법으로 각 유출성분의 고유한 화학적 조성을 기반으로 하는 추적자를 이용하는 방법(tracer-based method)이 있으며 유출성분을 분리하기 위해서는 각 성분마다 다양한 추적자를 이용하며, 여기에는 염화물(chloride), 안정 동위원소(stable isotopes), 방사성 동위원소(radioactive isotopes)와 같은 불활성 이온이 사용된다. 그러나 추적자로 이용하는 분리 방법은 시료 채취 및 검출에 높은 비용이 소요되어 장기간 분석에 한계가 있다. 한편, 하천유량의 EC는 지표수 유입시 비교적 낮은 반면 지하수 유입시 비교적 높은 값으로 변화되며, 이는 특정 시점의 유량 내 지표수와 지하수의 대략적인 비율을 추정할 수 있음을 의미한다.
Pinder and Jones(1969), Pilgrim et al.(1979), Matsubayashi et al.(1993), Cey et al.(1998), Yu and Schwartz(1999), Stewart et al.(2007) 등의 연구는 EC가 수문곡선에서 유출성분을 분리할 수 있는 환경지표로 사용될 수 있음을 나타내었다. 이들 연구에서 하천유량의 EC 값은 지표유출량과 반비례 관계에 있음을 나타내었다. 즉, 하천유량의 EC는 지표유출량이 증가함에 따라 급격히 떨어지고, 최대 유출이 발생하는 기간에 최솟값에 도달하며, 유출량이 감소함에 따라 비교적 느리게 증가하고 지표유출이 중단되면 최댓값에 도달하는 형태를 나타낸다.
CMB 방법은 다른 기저유출 분리 방법의 효과를 분석하거나 분리 방법의 매개변수를 보정하는 참고값으로 활용된 선행연구가 있으나(Stewart et al., 2007; Lott and Stewart, 2013; Lott and Stewart, 2016; Zhang et al., 2017; Saraiva Okello et al., 2018; Lyu et al., 2020), 유출성분별 EC를 추정하여 적용함에 따라 기저유출 분리 결과가 과다 또는 과소평가 될 수 있고, EC 데이터는 시간에 따라 변동할 수 있어 변동성을 충분히 반영하지 못하는 경우 정확성이 낮을 수 있다. 본 연구에서는 EC 시계열 자료의 시간 해상도 및 장기 연속성이 부족하여 CMB 방법을 적용하기 어려웠다. 향후 EC 기반 기저유출 분리 기법은 단기 집중 모니터링 및 전통적 분리기법과의 병행 적용을 통해 교차검증 또는 매개변수 보정 도구로 활용될 수 있을 것으로 판단된다(Stewart et al., 2007; Lott and Stewart, 2013).
2.4.기저유출 산정방법 및 평가지표
기저유출 분리 모형의 성능 평가는 관측값과 모의값 간의 정량적 유사성을 기반으로 이루어지며, 다양한 통계적 평가지표 중 NSE, RSR, PBIAS, KGE가 수문학 분야에서 널리 사용되고 있다. NSE와 KGE는 1에 가까울수록, RSR은 0에 가까울수록, PBIAS는 ±0%에 가까울수록 모형의 성능이 우수하다. Moriasi et al.(2007)은 이러한 지표들에 대해 수문 모델 성능 분류 지침을 제시하였으며, Knoben et al.(2019)은 KGE가 NSE보다 편향과 분산 오차까지 동시에 진단할 수 있다는 장점을 강조하였다. 본 연구에서는 이러한 평가지표들을 기반으로 기저유출 분리 모형의 성능을 비교하였으며, 해석 기준은 (Table 2)에 요약하였다.
2.5.관측 기저유량 추정 방법
기저유출 분리 모형의 성능을 평가하기 위해서는 모형에서 산정한 기저유량과 관측 기반의 기준값 간 적합성을 정량적으로 비교하는 과정이 필요하다. 그러나 실제 기저유량은 직접 측정이 불가능하기 때문에, 기존 연구에서는 건기 기간(dry season)의 하천 유량이나 최소 유량(minimum flow)을 대체값으로 활용하여 준관측값(proxy baseflow)을 구성하는 방식이 널리 사용되어 왔다(Kang et al., 2021).
본 연구에서는 영국 수문학회(UKIH: UK Institute of Hydrology)에서 제안한 smoothed minima 방법(Gustard et al., 1992)에 기반하여, 전체 유량 자료를 블록(block) 단위로 분할한 뒤, 각 블록 내 최소 유량 중 전일 유량 증가 등의 조건을 배제한 3~10개의 값을 선별하고, 이들을 연결하여 baseflow hydrograph를 구성하였다. 이러한 방식은 건기의 유량 중에서도 기저유량 특성을 반영할 수 있는 구간을 통계적으로 대표하는 자료를 확보하는 데 유리하며, 유역 특성과 계절성을 고려한 블록 크기 조정 및 기준 설정이 기저유출 분리의 신뢰도를 향상시킬 수 있음을 기존의 연구가 제시하고 있다(Aksoy et al., 2008).
또한, 캐나다 ORMGP(Oak Ridges Moraine Groundwater Program)의 감수곡선 분석 기법을 도입하여 하천 유량 자료로부터 감수 구간(recession segment)을 자동 추출하고, 회귀 분석을 통해 감수인자(k)를 산정하였다. 이 방법은 평가용 기저유량 참값 산정에도 활용 가능하다. 특히 홍수기의 영향 제거를 위해 초기 유량값은 해당 월 평균 유량의 2~3배 이하로 제한하여 이상치를 필터링하였다.
2.6.영산강·섬진강 유역 기저유출 분리 선정 유량관측소 및 유역특성인자 도출
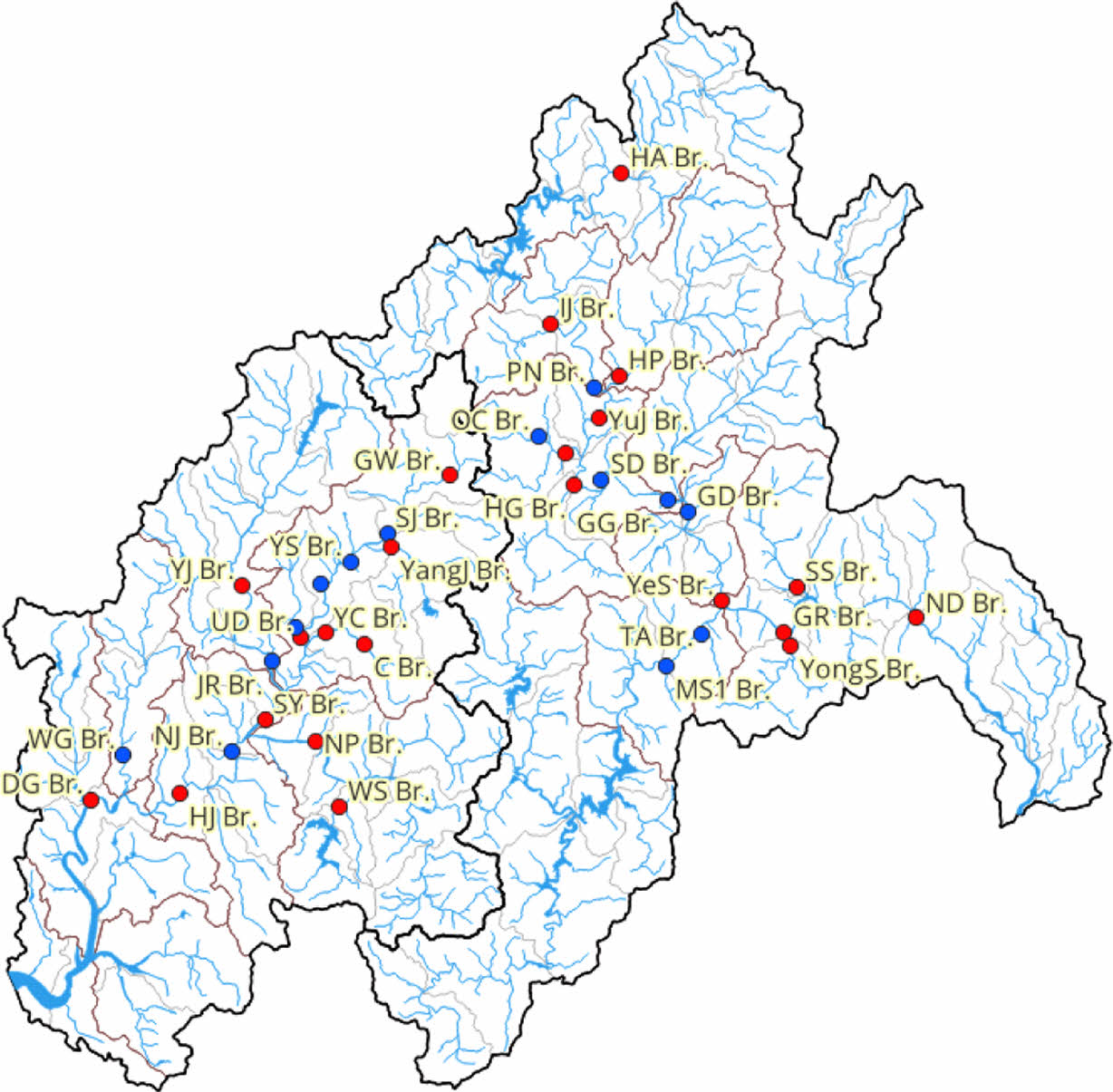
영산강 및 섬진강 유역의 기저유출 특성을 정량적으로 분석하기 위해 영산강홍수통제소에서 제공하는 수문자료(www.yeongsanriver.go.kr/sumun/wlList.do?S=S01) 조회를 통해 최근 5개년(2019-2023) 유량자료를 검토한 결과, 전체 70개 유량측정 지점 중 연속적인 자료가 확보된 14개소와 결측일을 보정하여 분석이 가능한 22개소를 포함한 총 36개 지점을 선정하였다(Fig. 1). 이들 지점은 영산강 및 섬진강 유역 각각 18개소로 균등하게 분포되어 있으며, 하천망 및 유역 대표성 등을 고려하여 결정되었다.
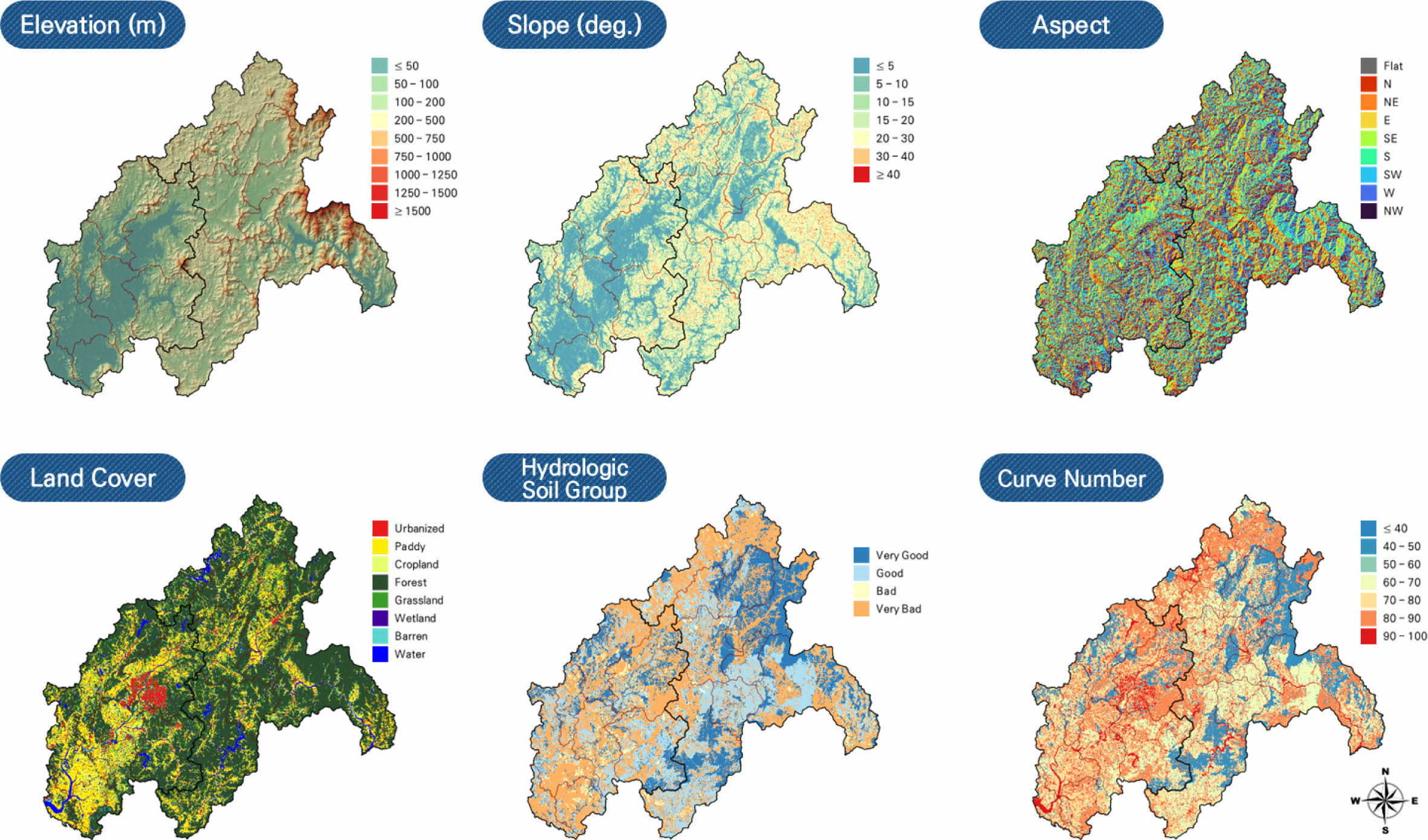
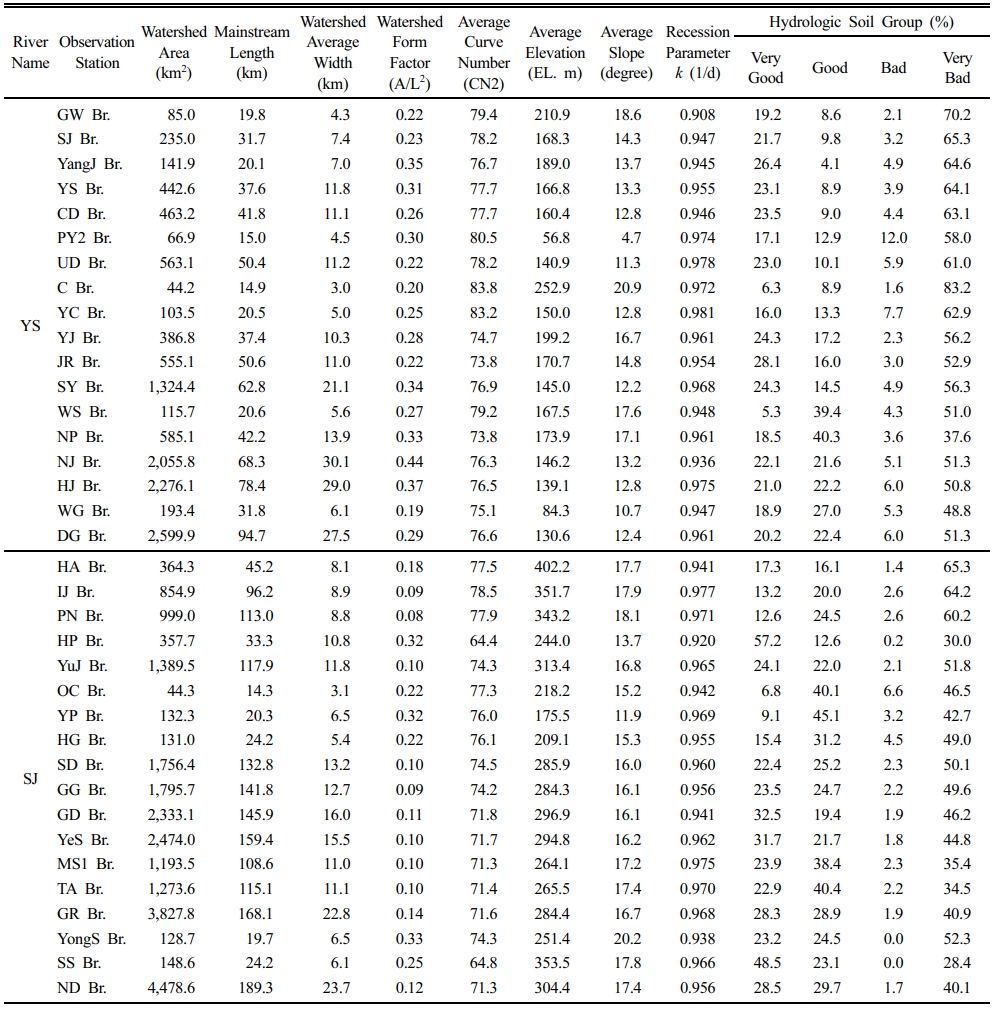
각 유역의 기저유출 특성과 관련된 인자를 도출하기 위해 수치표고모델(DEM), 토지피복도(Land Cover Map), 토양도(Soil Map) 등 공간자료를 기반으로 유역 경계 내에서 면적, 유로연장, 평균 경사, 표고, 곡률, 토지이용 유형, Curve Number, 수문학적 토양군(HSG) 등의 유역 특성 인자를 GIS 분석을 통해 정량화하였다(Fig. 2, Table 3). 본 연구에서는 토양의 침투능 및 유출 잠재성에 따라 A, B, C, D의 4가지 그룹을 A = very good, B = good, C = bad, D = very bad로 간주하여 제시하였다.
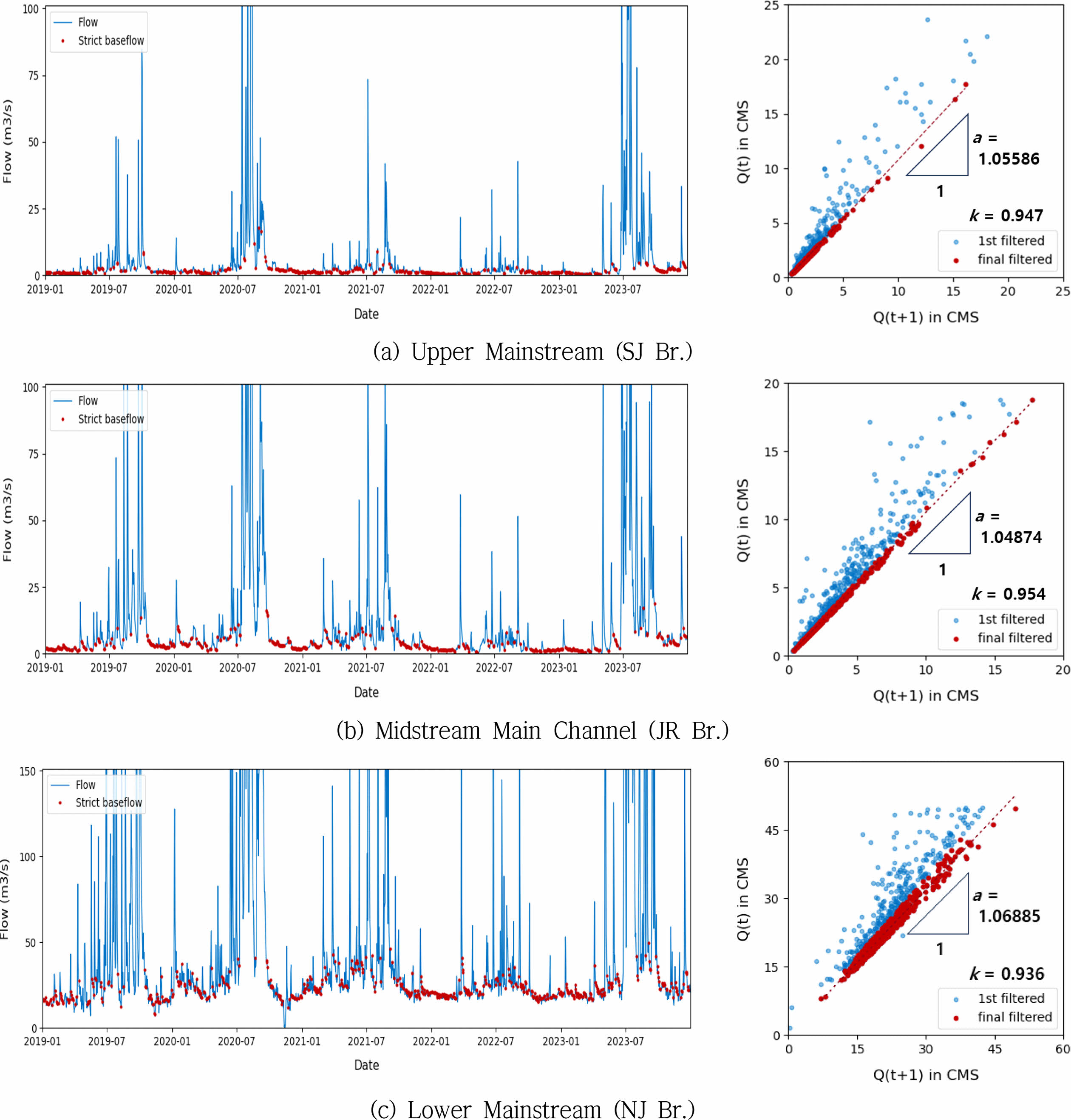
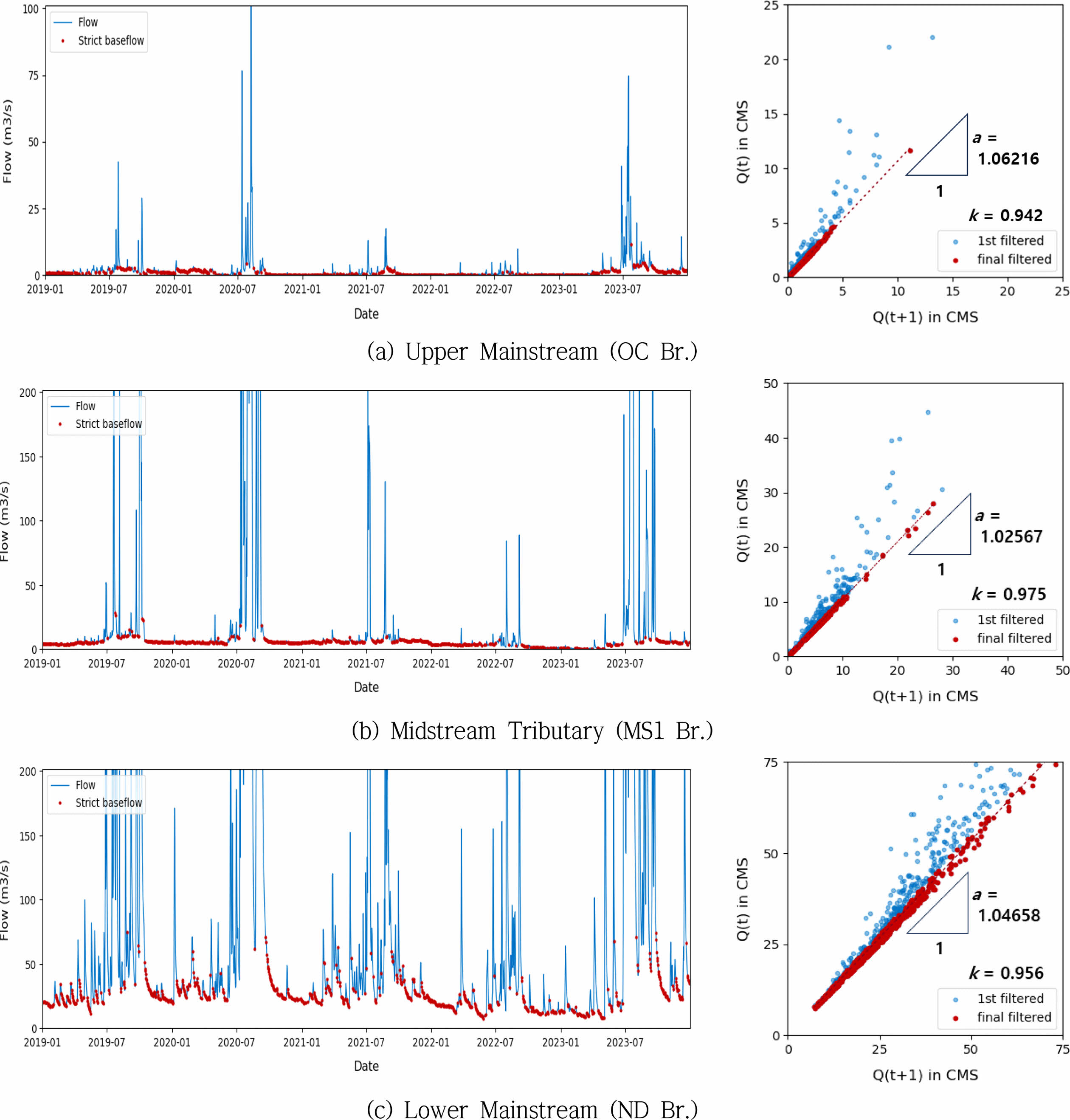
또한, 기저유출 구간에서 하천유량이 지수적으로 감소하는 현상을 수학적으로 설명하기 위해 감수 매개변수(recession parameter, k)를 유량 시계열로부터 자동으로 산정하였다. Qt+1 ≤ Qt에 해당하는 유량 감소구간을 필터링하고 Eq. (2)와 같은 선형회귀분석을 결정계수(R2)가 0.995를 초과 시 까지 반복 수행 함으로써 유량 감소구간의 선형성을 잘 나타내는 데이터를 자동으로 선별 후, 절편 b를 0으로 하는 선형 회귀계수 a를 산정 후 Eq. (3)과 같이 기울기 a의 역수를 취하는 방법으로 k를 산정하였다. 유역별 비교 결과는 Table 3에, 상·중·하류 대표 지점에 대한 시간별 감소 특성은 Fig. 3 및 Fig. 4에 도시하였다.

|
Fig. 1 Study Sites for baseflow separation in the yeongsan and seomjin watersheds. |
|
Fig. 2 Analysis of characteristics in the yeongsan and seomjin watersheds. |
|
Fig. 3 Estimation results of recession parameters (k) at representative points in the upper, middle, and lower reaches of the yeongsan watersheds. |
|
Fig. 4 Estimation results of recession parameters (k) at representative points in the upper, middle, and lower reaches of the seomjin watersheds. |
|
Table 1 Major Baseflow separation methods based on digital filtering techniques |

|
|
Table 2 Performance evaluation metrics for baseflow separation models |
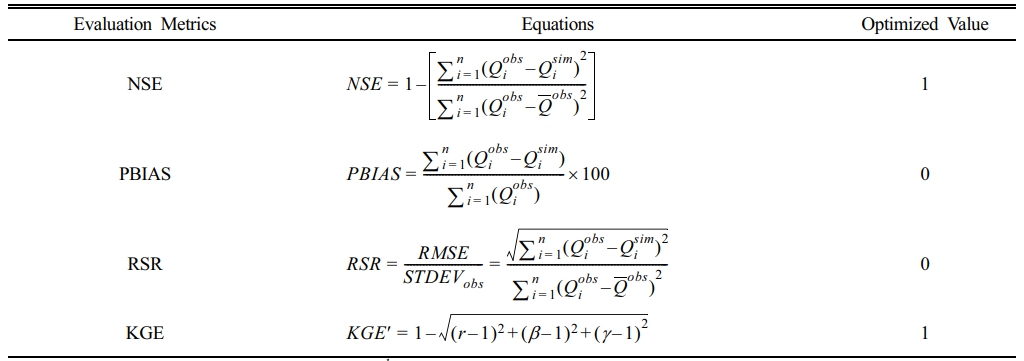
Qiobs: observed value, Qisim: simulated value, Q-obs: mean of observed value, n: number of samples, r: correlation coefficient, β : bias, γ : variability |
|
Table 3 Results of monitoring station and watershed characteristics analysis for baseflow analysis in the yeongsan and seomjin watersheds |
3.1.도식적 방법 적용 결과
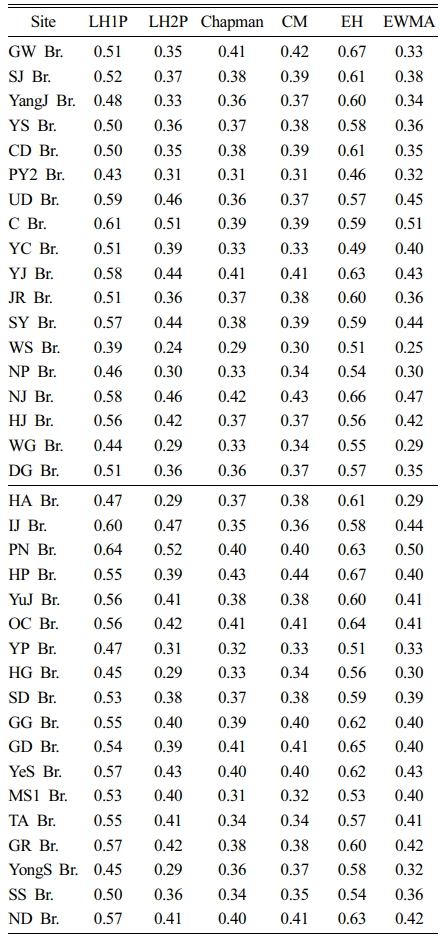
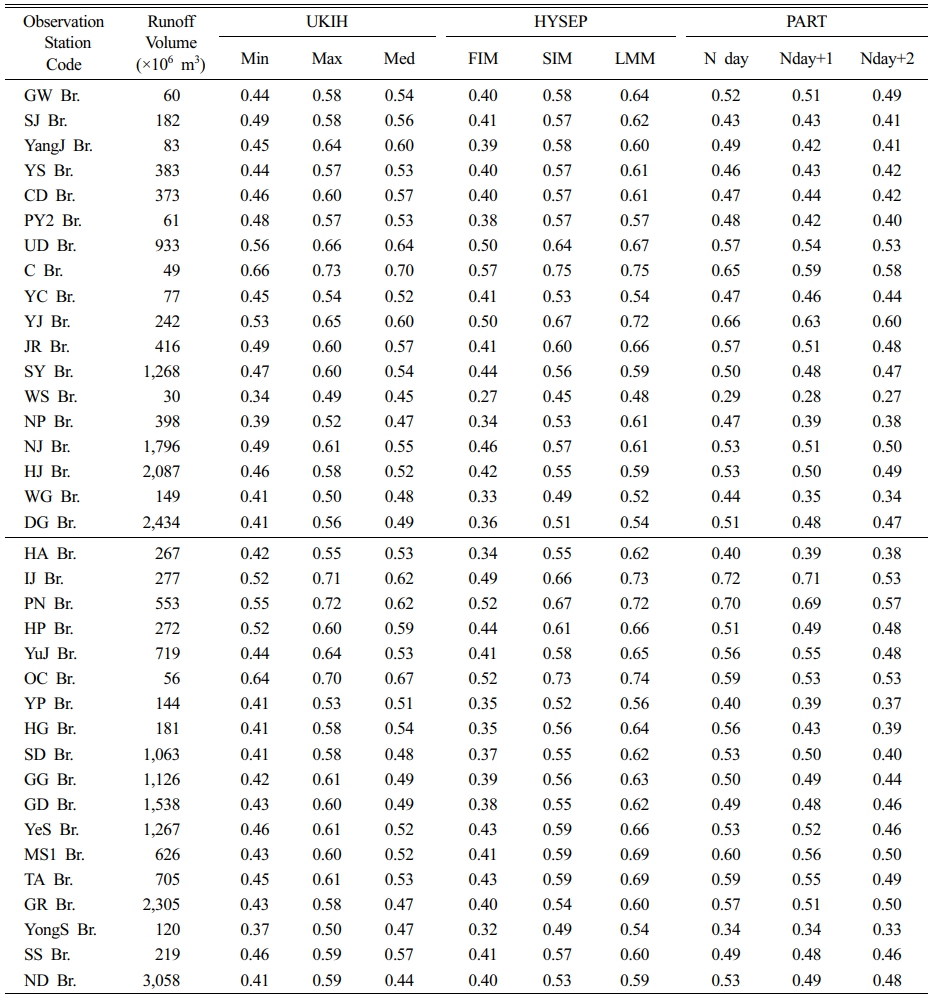
영산강 및 섬진강 유역의 36개 유량관측소에 대해 도식적 분리기법을 적용하여 산정한 기저유출지수는 (Table 4)에 정리하였다. 분석 결과, 전체 BFI는 영산강 유역에서 0.41~0.61, 섬진강 유역에서는 0.41~0.64 범위로 나타나 두 유역 모두 유사한 수준의 기저유출 비율을 보였다. 도식적 방법별로는 영산강 유역에서 HYSEP-SIM이 0.45~0.75로 가장 높은 BFI를 산출하였으며, HYSEP-FIM은 0.27~0.57로 가장 낮은 값을 보였다. 반면, 섬진강 유역에서는 HYSEP-LMM이 0.54~0.74로 가장 높은 값을 나타냈고, HYSEP-FIM은 0.32~0.52로 가장 낮았다. 이는 동일 유역 내에서도 적용된 도식적 방법의 차이에 따라 기저유출 산정 결과에 유의미한 편차가 발생할 수 있음을 보여준다. HYSEP의 세 가지 기법은 각각 최소값 탐색 방식, 시간 간격 설정 방식 등에 따라 민감도가 달라 BFI 결과에 영향을 미치는 것으로 알려져 있다(Nathan and McMahon, 1990; Sloto and Crouse, 1996).
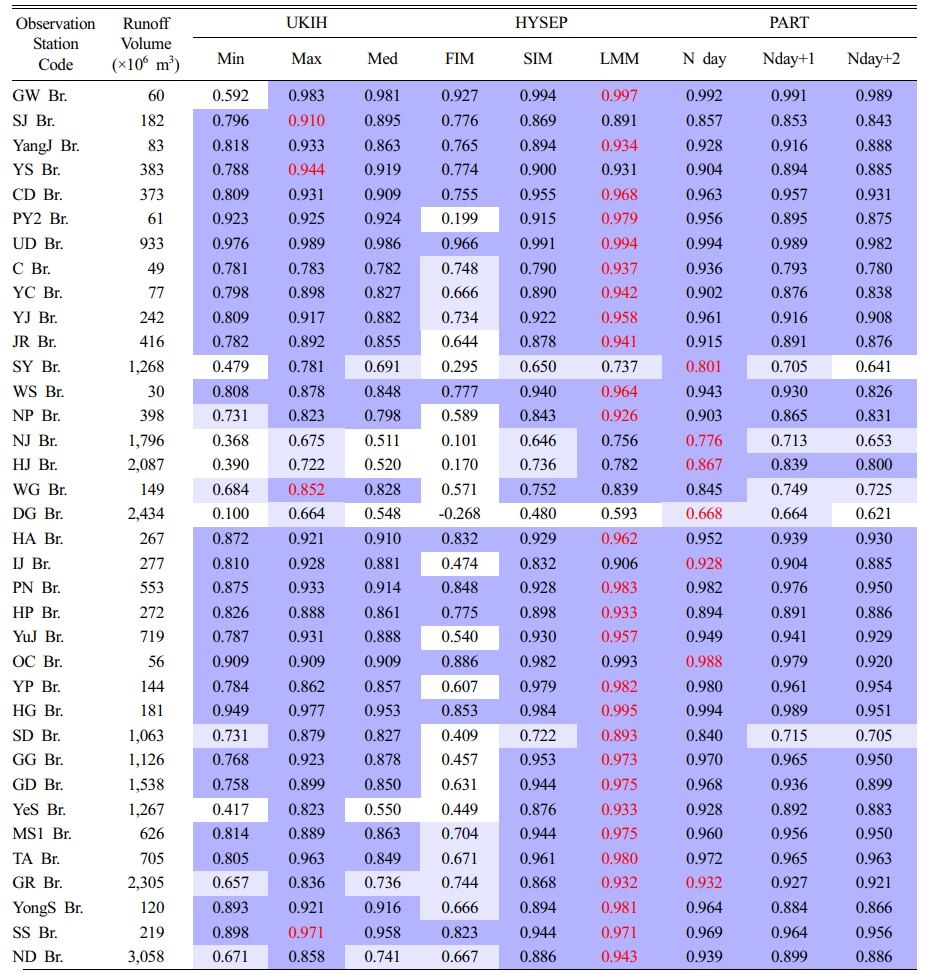
각 기저유출 분리 방법의 정확도와 적합도는 대표적인 통계적 평가지표인 NSE(Nash-Sutcliffe Efficiency), PBIAS, KGE, RSR를 통해 비교 분석하였다. 분석 결과, RSR 지표는 모든 방법에서 ‘매우 양호(very good)’ 수준(< 0.5)을 기록하여, 상대적 방법 간 성능 구분에는 한계가 있는 것으로 나타났다. 반면, PART 및 HYSEP-LMM 방법은 NSE가 0.75 이상(Table 5 참조), PBIAS가 ±5% 이내로 나타나는 등 전반적인 평가지표에서 우수한 평가를 받아 상대적으로 높은 신뢰성을 보였다(Rutledge, 1998; Sloto and Crouse, 1996). 이에 반해, UKIH-Min 및 HYSEP-FIM 방법은 모의 기저유출이 과소 또는 과대 산정되는 경향을 보여 전체적으로 낮은 NSE 및 KGE 값을 기록하였으며, 관측값과의 편차가 비교적 커서 모형 재현성 측면에서 제한점이 있는 것으로 평가되었다.
이러한 경향은 기존 연구에서도 확인된 바 있으며(Sloto and Crouse, 1996; Kang and Lee, 2021), 특히 HYSEP-FIM 및 UKIH-Min과 같은 규칙 기반 도식적 방법은 하천유량의 잡음 또는 단기 강우 반응에 민감하여 기저유출을 과소 추정하는 경향이 있다. 본 연구 결과는 다양한 방법 간 BFI 산정의 민감도를 실증적으로 나타내므로 유역의 지형·토양·유량 특성에 따라 적절한 분리 방법을 선택하는 것이 중요함을 시사한다.
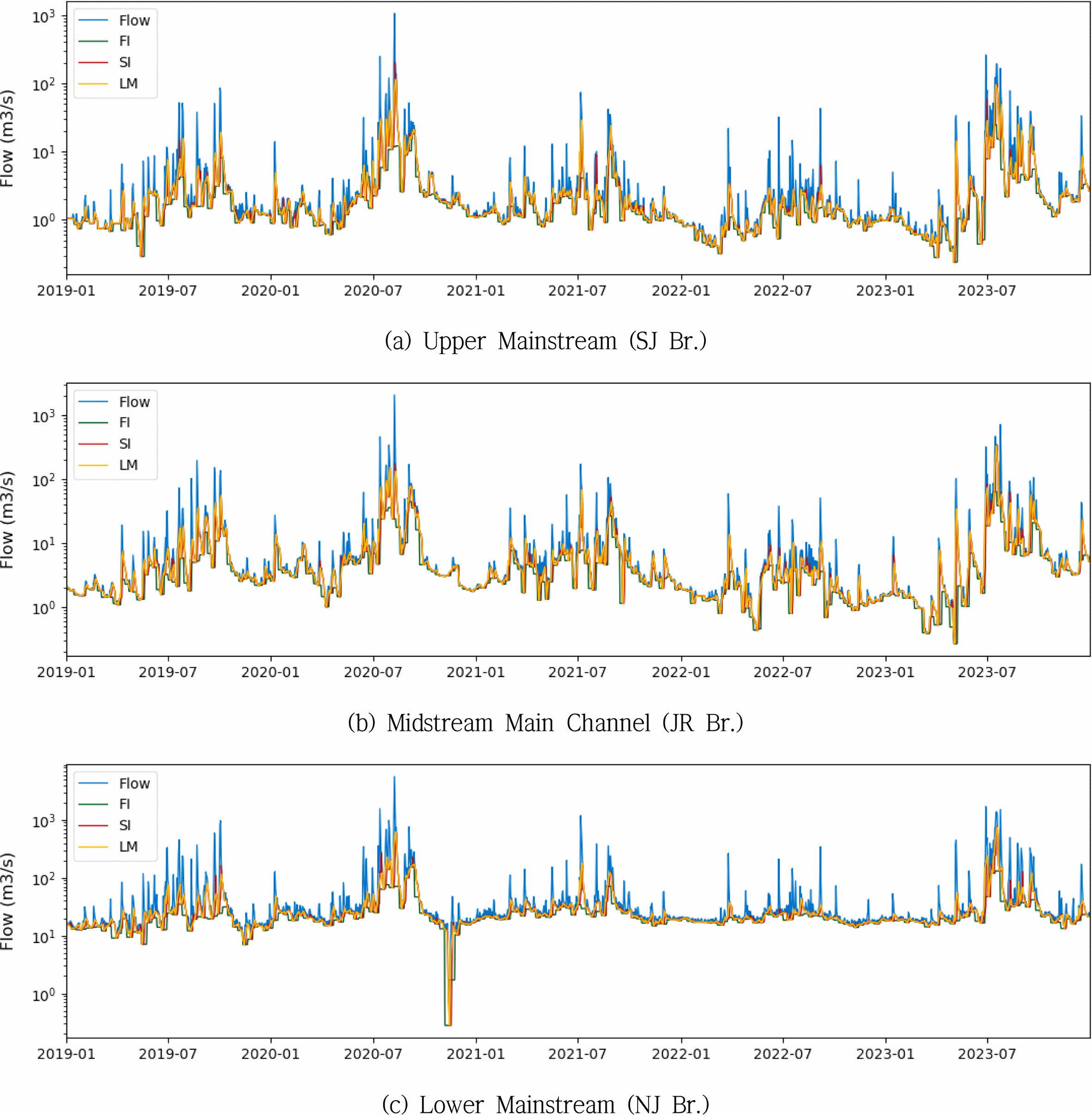
동일 유역 내에서도 BFI 산정값이 방법에 따라 상당히 달라질 수 있으므로, NSE, PBIAS, KGE 등의 평가지표를 종합적으로 활용한 정량적 평가가 필수적이다(Knoben et al., 2019). 본 연구에서는 상대적으로 우수한 성능을 나타낸 HYSEP-LMM 방법을 활용하여 영산강 및 섬진강 유역의 상·중·하류 대표 지점에 적용하였으며, 해당 결과는 (Fig. 5) 및 (Fig. 6)에 제시하였다.
HYSEP-LMM 기법이 상대적으로 우수한 성능을 보인 이유는, 일시적인 유량 급변보다 일정 구간 내의 최저 유량을 기반으로 기저유출을 산정함으로써 지하수 기반의 지속적인 유출 특성을 보다 현실적으로 반영하기 때문이다(Sloto and Crouse, 1996; Kang and Lee, 2021). 특히, 이 방법은 강우 후 유량 급등이나 단기 잡음에 민감하지 않아, 장기적인 기저유출 패턴을 안정적으로 도출하는 데 유리한 특성이 있다. 따라서, 중규모 유역인 영산강 및 섬진강 유역의 유량 특성과 지형 특성에 부합하며, 일별 유량 자료에서도 통계적으로 우수한 BFI 결과를 제공하였다. 결론적으로 HYSEP-LMM 방법은 영산강 및 섬진강 유역의 수문학적 현실성과 통계적 적합성을 모두 충족시키는 기법으로 평가된다.
3.2.디지털 필터 방법 매개변수 민감도 분석
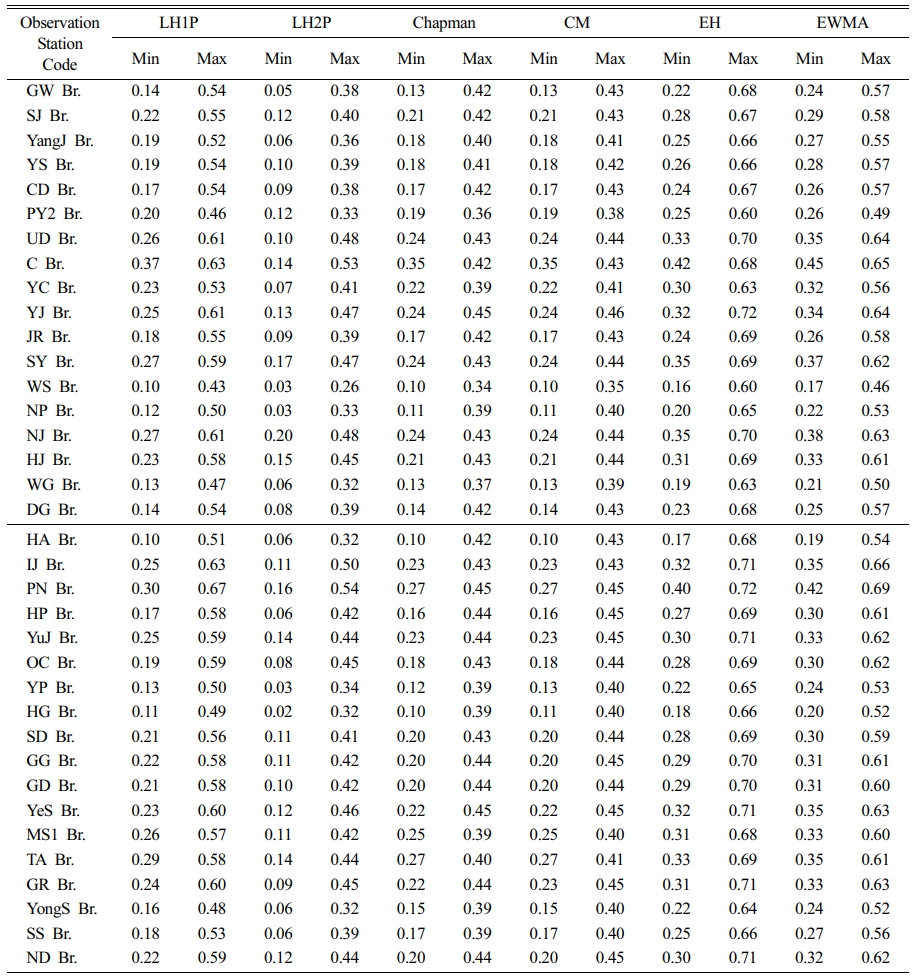
본 연구는 디지털 필터 기반의 기저유출 분리법의 적용 타당성과 신뢰도를 평가하기 위해, 36개 유량관측소에 대해 매개변수 민감도 분석을 수행하였다(Table 6, Figs. 7 & 8 참조). 적용된 6가지 필터 방법(LH1P, LH2P, Chapman, CM, Eckhardt, EWMA)에 대해 감수상수 α 및 최대 기저유출지수 BFImax의 변화에 따른 BFI 민감도를 분석한 결과, EWMA를 제외한 대부분의 필터에서는 매개변수 증가에 따라 BFI가 감소하였다. 이는 α 값이 커질수록 필터의 민감도가 낮아져 더 많은 유량이 직접유출로 분리되기 때문으로 해석된다. 반면, EWMA는 지수 가중 방식의 구조적 특성으로 인해 최근 유량에 대한 반응성이 높아지며, 기저유출로 간주되는 유량이 증가하는 경향을 보였다. 이러한 차이는 필터 알고리즘의 수학적 구조에 따른 특성으로, 필터 선택 시 유역 특성과 민감도 특성을 고려한 접근이 필요함을 시사한다(Eckhardt, 2005; Tularam and Ilahee, 2008; Lyu et al., 2020).
디지털 필터 기반 기저유출 산정 과정에서는 동일한 유량 자료에 대해서도 매개변수 설정값에 따라 ±0.1 이상의 BFI 차이가 발생하는 사례가 다수 확인되었다. 이는 필터 알고리즘이 매개변수 변화에 민감하게 반응하는 구조적 특성 때문으로, 경험적 설정값보다는 유역 특성을 반영한 최적 매개변수의 산정이 필수적이다. 특히 Eckhardt 필터와 같이 복수의 매개변수를 포함하는 경우, 수치 최적화 또는 교차검증 기반의 정량적 보정이 필요하다(Eckhardt, 2005; Lott and Stewart, 2013). 디지털 필터 방식은 자동화에 유리하다는 장점이 있지만, 민감도 특성을 무시할 경우 BFI 산정에 오류가 발생하여, 결과적으로 수문모형, 수자원 계획, 생태유량 평가 등 후속 해석의 정확도를 저하시킬 수 있다. 따라서 민감도 분석과 현장 교차검증을 병행한 보정 절차를 통해 매개변수를 설정하는 것이 바람직하며, 필요시 EC 기반 관측값을 활용한 교차 보정 전략도 고려되어야 한다.
본 연구에서 수행한 디지털 필터 기반 매개변수 민감도 분석 결과, 동일 유량 자료에 대해서도 매개변수 설정값에 따라 BFI 산정 값이 ±0.1 이상 차이를 보이는 사례가 다수 확인되었다. 이는 기저유출 분리 시 매개변수 설정의 민감도를 충분히 고려하지 않을 경우, 산정 결과의 신뢰성에 왜곡이 발생할 수 있음을 시사한다. 따라서 향후 기저유출 분리방법을 선정 시 유역 특성에 부합하는 디지털 필터 방법을 적용하고, 필터 매개변수에 대한 교차검증 및 민감도 분석을 병행한 정량적 보정 절차가 필수적이다. 궁극적으로는 각 분리기법의 수학적 구조와 한계를 명확히 이해한 후, 정량적 매개변수 보정을 통해 보다 정확하고 신뢰도 높은 수문학적 해석이 가능할 것으로 판단된다.
3.3.디지털 필터 방법 적정 매개변수 추정
디지털 필터 기반 기저유출 분리 기법에서는 매개변수 설정이 결과에 직접적인 영향을 미치므로, 민감도 분석을 통해 적절한 값을 도출하는 과정이 필수적이다. 대부분의 필터는 단일 매개변수(예: Lyne-Hollick의 a또는 EWMA의 e)를 사용하며, Lyne-Hollick 방법의 경우 Nathan & McMahon(1990)은 다양한 유역에서 안정적인 성능을 보인 α = 0.925를 권장값으로 제안하였다. 한편 Eckhardt 방법은 감수상수 α와 최대 기저유출지수 BFImax의 두 매개변수를 필요로 하며, 본 연구에서는 상시 유출이 발생하는 투수성 높은 대수층 특성을 반영하여 BFImax = 0.80을 적용하였다. 이와 같은 매개변수 설정은 디지털 필터 방법의 신뢰성과 현실 적합성을 향상시키기 위한 필수적인 절차이다.
민감도 분석 결과, 참값으로 간주된 기저유량과 필터링에 따른 기저유량 간의 유사도를 평가한 결과, 일부 지점(예: 남원시 SD Br.)에서는 매개변수 변화에 따른 뚜렷한 최적값 도출이 어려웠다. 반면, 대부분의 지점에서는 매개변수 증가에 따라 NSE 및 KGE 값이 점진적으로 감소하거나 일정 수준에서 안정화되는 경향을 보였다. 이에 따라, 본 연구에서는 필터 방법별 민감도 분석 결과를 바탕으로 적정 매개변수를 설정하였다. Lyne-Hollick 1-Pass 및 2-Pass 방법은 기존 연구(Nathan and McMahon, 1990)에서 제안된 α = 0.925를 적용하였고, Chapman 및 Chapman-Maxwell 방법은 유역별 감수상수를 기반으로 α 값을 설정하였다. Eckhardt 방법은 감수상수 α를 감수곡선 분석 결과를 반영하여 설정하고, BFImax는 공극률이 높은 대수층 조건을 반영하여 0.80을 적용하였다(Eckhardt, 2005). EWMA 방법은 ε = 0.015를 최종 적용하였으며, 이는 0.005~0.015의 범위 내에서 민감도 분석을 통해 결정한 값이다(Tularam and Ilahee, 2008). 이러한 매개변수 설정은 각 유역의 수문 특성을 반영한 합리적 기준으로, 디지털 필터 방법의 정확성과 신뢰성을 제고하는 데 기여한다.
한편, 디지털 필터 방법의 민감도 분석 결과, 다수의 지점에서 매개변수 변화에 따라 NSE, KGE 등의 평가지표가 완만하게 변화하거나 명확한 최적값을 나타내지 않는 경향이 관찰되었다. 이러한 현상은 디지털 필터가 유량 시계열에 대해 일정한 규칙으로 필터링을 수행하는 구조적 특성에 기인하며, 수치 최적화를 통한 정밀한 보정보다는 기존 문헌에서 제시된 권장값이나 유역 특성에 기반한 간접 추정 방식이 실용적인 대안이 될 수 있음을 시사한다. 이에 본 연구에서는 각 디지털 필터 방법에 대해 문헌에서 제안된 추천값 및 유역의 감수 특성을 반영하여 매개변수를 설정하였으며, 이러한 접근은 향후 다양한 유역 유형에 대한 적용성 확대 및 비교 연구 수행에 있어 실질적인 기준점을 제공할 수 있을 것으로 판단된다.
3.4.디지털 필터 방법 적용 결과 및 최적 산정방법 선정
디지털 필터 기반 기저유출 분리 방법의 비교 분석을 위해 총 6개의 필터 기법에 대해 민감도 분석을 통해 도출된 매개변수를 적용하여 BFI를 산정하였다(Table 7 & Figs. 9-12 참조). 전체 36개 분석 지점에서 산출된 BFI는 0.24에서 0.67의 범위를 나타냈으며, 유역 및 방법별로 상이한 분포 특성을 보였다. 방법별 성능 비교 결과, Lyne-Hollick 2-Pass(LH2P), Chapman, Chapman-Maxwell(CM) 방법은 NSE, PBIAS, KGE 등의 평가지표에서 전반적으로 낮은 적합도를 보여 연구 대상 유역의 수문 특성을 충분히 반영하지 못한 것으로 해석된다. 반면, Lyne-Hollick 1-Pass(LH1P) 및 Eckhardt(EH) 방법은 비교적 안정적인 BFI 산정 결과를 제공하였으며, 다수 지점에서 높은 적합도와 일관된 성능을 나타냈다. Lyne-Hollick 방법은 간편성과 보편성으로 인해 널리 사용되고 있으나, Chapman(1999)은 이 방법이 이론적으로 기저유출을 과대 또는 과소 추정할 가능성이 있음을 지적한 바 있다. 또한, 국내 연구(Kang et al., 2022)에서도 실측 기반 검증 시 일관된 기저유출 분리를 보장하지 못한다는 결과가 보고된 바 있다. 이러한 결과는 디지털 필터 방식의 적용 시 유역 특성과 방법 간 상호작용을 고려한 세심한 판단이 필요함을 시사한다. Fig. 10 Fig. 11
본 연구에서는 앞선 비교 분석 결과와 기존 문헌에서의 평가를 종합적으로 고려하여 Eckhardt 방법을 연구 대상 유역의 최적 기저유출 분리 기법으로 선정하였다(Table 7 참조). Eckhardt 방법을 적용하여 2019년부터 2023년까지 5개년간 산정된 연평균 BFI는 영산강 유역의 경우 0.46에서 0.67의 범위로 나타났으며, 평균 BFI는 0.58로 분석되었다. 또한, 섬진강 유역에서는 0.51에서 0.67 사이의 값을 보였으며, 평균 BFI는 0.60으로 나타났다. 이와 같이 두 유역 모두 지점 간 BFI에는 일정한 편차가 존재하지만, 전체 평균값은 유사한 수준을 보였다. 이러한 결과는 영산강과 섬진강 유역이 전반적으로 안정적인 기저유출 특성을 공유하고 있음을 시사하며, 지형·지질적 조건, 토지피복, 강우 특성 등의 수문·환경 요인이 일정 수준 이상 유사함을 간접적으로 보여주는 지표로 해석될 수 있다.
Eckhardt 방법에 의해 산정된 BFI는 향후 수문 모델링, 수질 모의, 저수지 운영 전략 수립 등 다양한 수자원 관리 분야에서 기준값으로 활용될 수 있는 실질적 자료로서의 활용 가능성이 크다. 또한, 본 연구에서와 같이 유역 특성에 기반한 매개변수 설정과 함께 적용되는 경우, 기저유출 분리의 신뢰성을 향상시킬 수 있으며, 유역 유형별 적용성 확대 및 비교 연구 수행을 위한 실증적 기준점을 제시할 수 있다는 점에서 중요한 의미를 갖는다. 아울러, BFI의 연도별 변화 추이를 장기적으로 분석할 경우 지하수 유출의 변화 경향을 파악할 수 있으며, 기후변화나 토지이용 변화와 같은 외부 요인에 따른 유역의 수문 반응 민감도를 진단하는 데에도 유용하게 활용될 수 있다. 이와 같은 점에서, 본 연구 결과는 단순한 기저유출 산정에 그치지 않고, 유역 수문 특성 이해와 향후 수문학적 모델링 정교화에도 기여할 수 있는 기반자료로 평가된다.
3.5. 유역별 기저유출 영향인자 도출
본 연구에서는 기저유출 특성에 영향을 미치는 요인을 규명하기 위해, 총 36개 유량관측 지점을 대상으로 BFI와 다양한 유역 및 하천 특성 인자 간의 상관관계를 분석하였다. 이를 위해 GIS 기반의 공간 분석을 통해 유역 면적, 유로 연장, 평균 폭, 평균 표고, 평균 경사, 토지피복 유형(산림, 시가화, 농경지 등), 수문학적 토양군, 유출계수 등의 인자를 산정하였으며, 이들 변수와 BFI 간의 관계를 통계적으로 비교하였다.
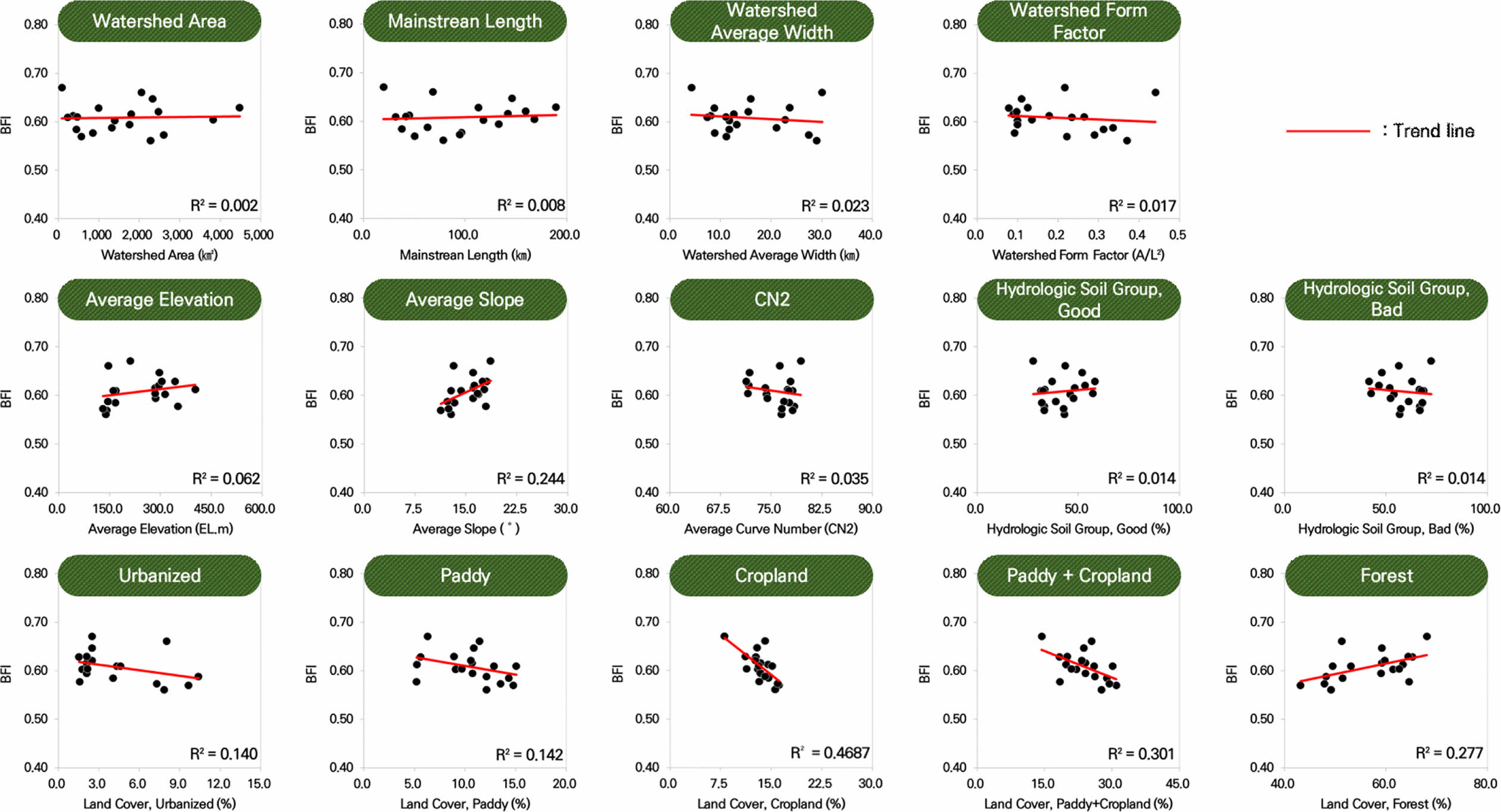
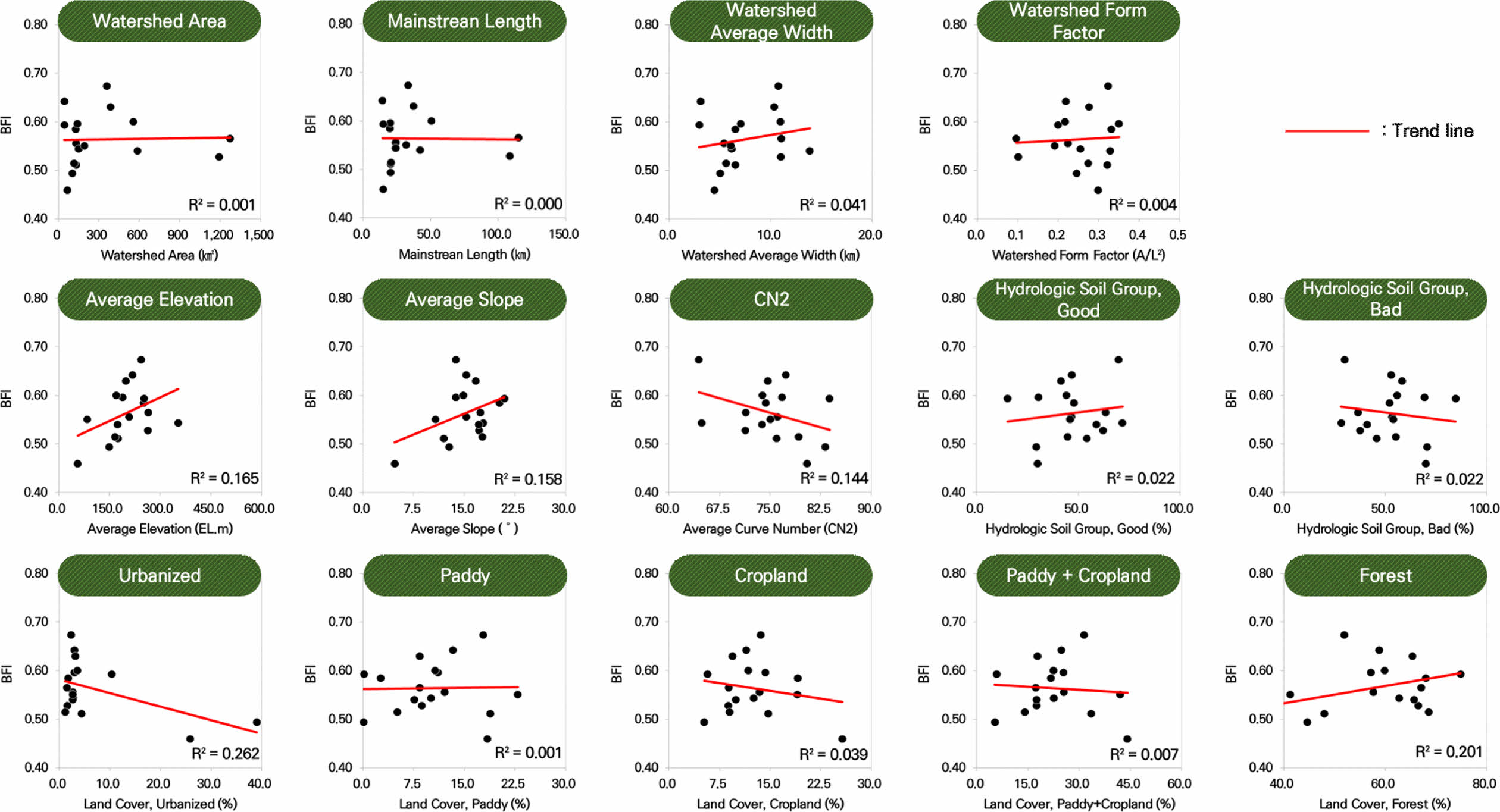
Figs. 13-14에 제시된 단순 상관분석 결과, 전체적으로 유역 특성과 BFI 간에는 뚜렷한 상관성이 나타나지 않았다. 그러나 보다 정밀한 해석을 위해 유의수준 0.05(신뢰수준 95%)를 기준으로 t-검정을 실시한 결과, 일부 유역 특성 인자와 BFI 간에 통계적으로 유의한 관계가 확인되었다(Table 8 참조). 예를 들어, 산림 면적 비율이 높은 유역에서는 BFI 값이 유의하게 높게 나타났으며, 이는 산림이 침투량을 증가시켜 지하수 함양을 촉진한다는 기존 연구 결과와 일치한다. 또한, 경작지 비율이 높은 유역에서도 BFI 증가 경향이 관측되었는데, 이는 경작지가 토양의 침투성을 높이고 지하수 함양에 긍정적으로 작용할 수 있음을 시사한다. 이러한 경향은 여러 국내외 회귀분석 기반 연구를 통해서도 보고된 바 있다.
예컨대, Zhang et al.(2013)은 미국 미시간 주 17개 유역을 대상으로 회귀모형을 분석한 결과, 경작지 비율, 모래 함량, 유효 강우량 등이 BFI의 유의미한 설명 변수로 작용하였으며, 평균 BFI는 0.71로 나타났다. 추가적으로 Ahiablame et al.(2013)은 경작지 비율이 BFI에 대해 양(+)의 회귀계수를 갖는다고 보고하였으며, R2 값은 0.17에서 0.57의 범위로 나타나 회귀모형의 설명력을 뒷받침하였다.
한편, 유출계수(runoff coefficient)가 낮은 유역일수록 BFI 값이 높은 경향이 관찰되었는데, 이는 지표 유출이 적고 지하수 유입이 상대적으로 많은 유역의 특성을 반영하는 것으로 해석된다. 이러한 분석 결과는 기저유출에 영향을 미치는 주요 인자를 규명하는 데 기여하며, 향후 유역 기반 수문관리 및 수자원 계획 수립에 있어 유용한 기초자료로 활용될 수 있다.
본 연구에서는 영산강과 섬진강 유역의 기저유출 특성을 분석하기 위해 다양한 유역 특성 인자와 기저유출지수(BFI) 간의 상관관계를 검토하였다. 그 결과, 본류 구간에서는 평균 경사, 밭 및 농지, 산림 비율 등이 일부 통계적으로 유의한 변수로 도출되었다. 이는 산림 비율이 높은 유역에서 BFI가 상대적으로 높게 나타나는 경향과 일치하며, 산림이 지하수 함양에 긍정적인 영향을 미친다는 기존 연구 결과와도 부합한다. 그러나 지류 또는 섬진강 유역에서는 유역 규모가 작고 지질 구조가 복잡하게 분포하며, 관개 및 배수시설 등 인공요인의 영향이 커 단일 유역 특성 인자로는 기저유출 변동성을 설명하는 데 한계가 있었다. 따라서 이러한 지역의 기저유출 예측에는 지하수위, 불투수율, 지역 인공시설 운영 정보 등을 포함한 다요인 통합분석이 필요하다. 특히 섬진강 유역은 산림 비율이 높고 시가화율이 낮은 특성을 가지나, 유역 규모가 작고 지질이 다양하게 분포하는 특성으로 인해 단일 변수로 기저유출을 설명하는 데 한계가 있는 것으로 판단된다. 따라서 이러한 유역에서는 기저유출 예측 시 물리적 인자 외에도 지하수위, 토양수분, 기상 조건 등 다양한 정보를 통합적으로 고려할 필요가 있다.
종합적으로 볼 때, 유역 평균 표고, 경사, 산림 및 시가화 비율은 기저유출에 일정 수준의 영향을 미치는 것으로 분석되었으나, 유역별 경향은 다양하게 나타나므로 단일 인자보다는 복합적인 요인 분석이 필요하다. 본 연구에서 도출한 유역별 BFI 값은 향후 수문모형 구축, 수질 오염물질 희석 예측, 생태유량 유지 기준 설정 등 유역 단위 통합 물관리에 있어 기초자료로 활용될 수 있다. 특히 Eckhardt 방법으로 산정된 BFI의 안정성은 영산강·섬진강 유역의 중·장기 수문 예측 기반자료로서 유의미하다. 향후 기저유출 예측 모델을 개발하거나 수문 모형에 적용할 경우, 이러한 다요인적 접근을 기반으로 한 정량적 분석이 요구되며, 이는 물순환 및 수자원 관리를 위한 정책 수립에도 중요한 시사점을 제공할 수 있다.
|
Fig. 5 Baseflow estimation results using the HYSEP method in the yeongsan watersheds. Note: FI (Fixed-Interval Method), SI (SlidingInterval Method), LM (Local Minimum Method) |
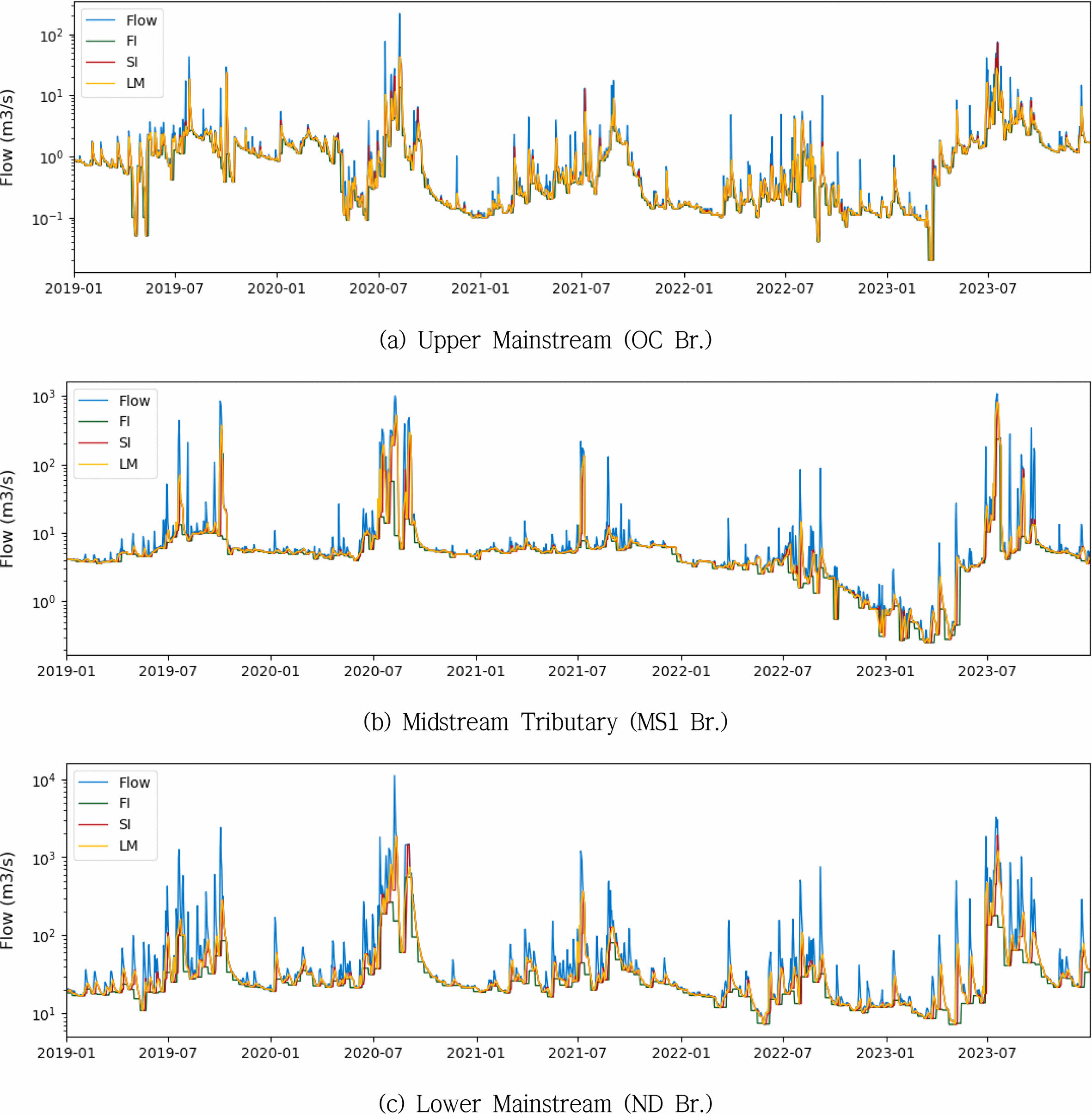
|
Fig. 6 Baseflow estimation results using the HYSEP method in the seomjin watersheds. Note: FI (Fixed-Interval Method), SI (SlidingInterval Method), LM (Local Minimum Method) |
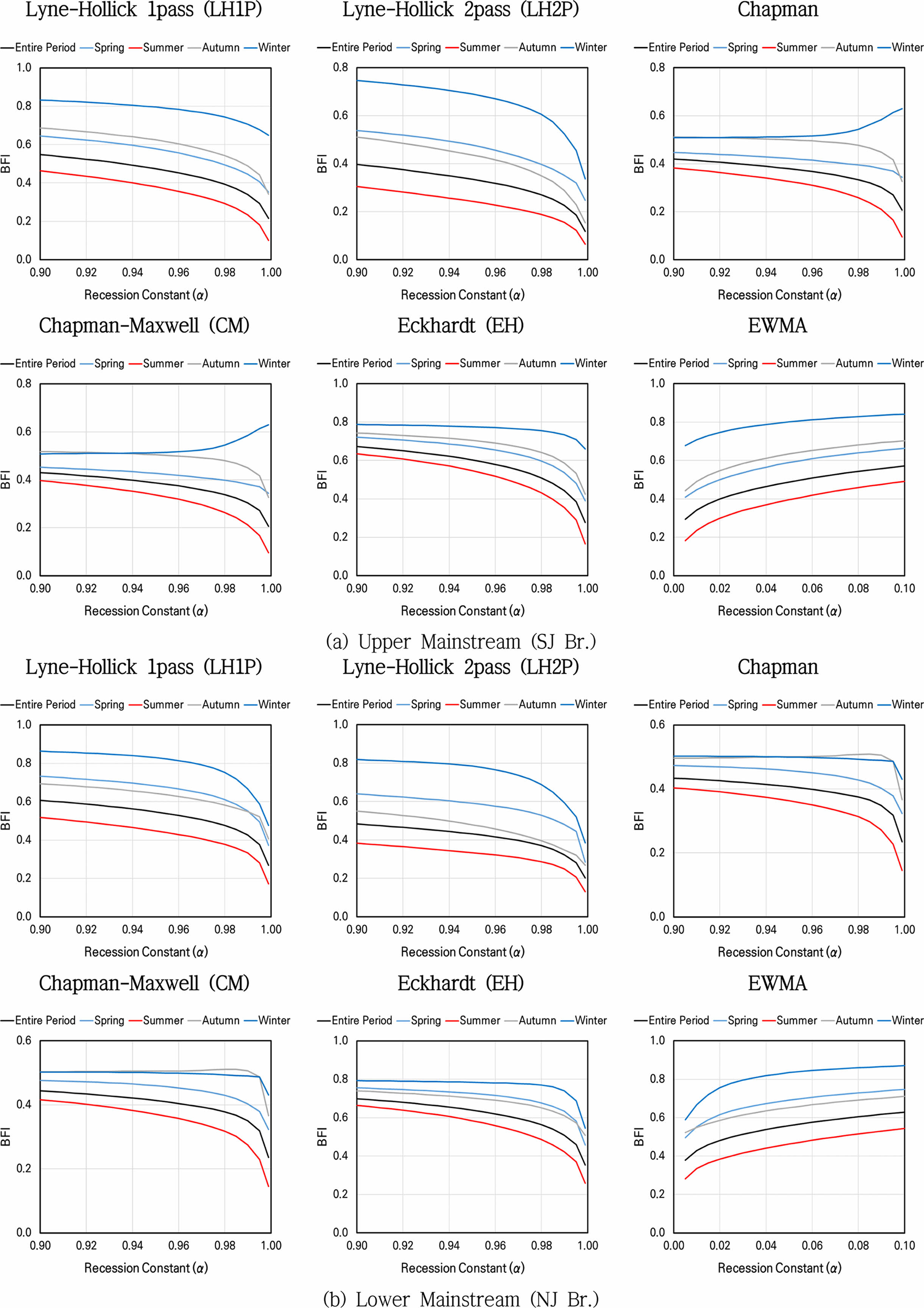
|
Fig. 7 Changes in baseflow index with parameter variations in the yeongsan watersheds |
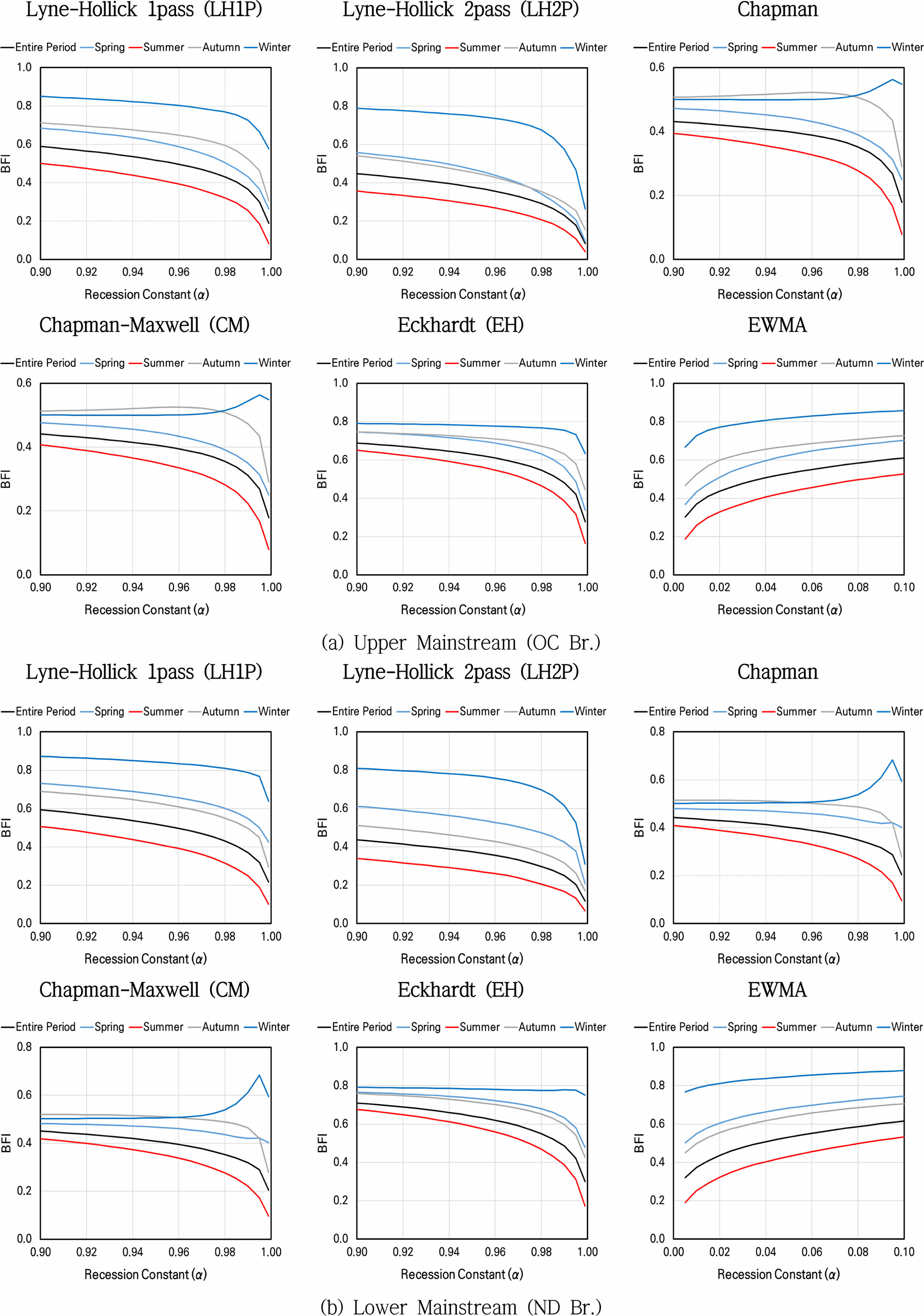
|
Fig. 8 Changes in baseflow index with parameter variations in the seomjin watersheds |
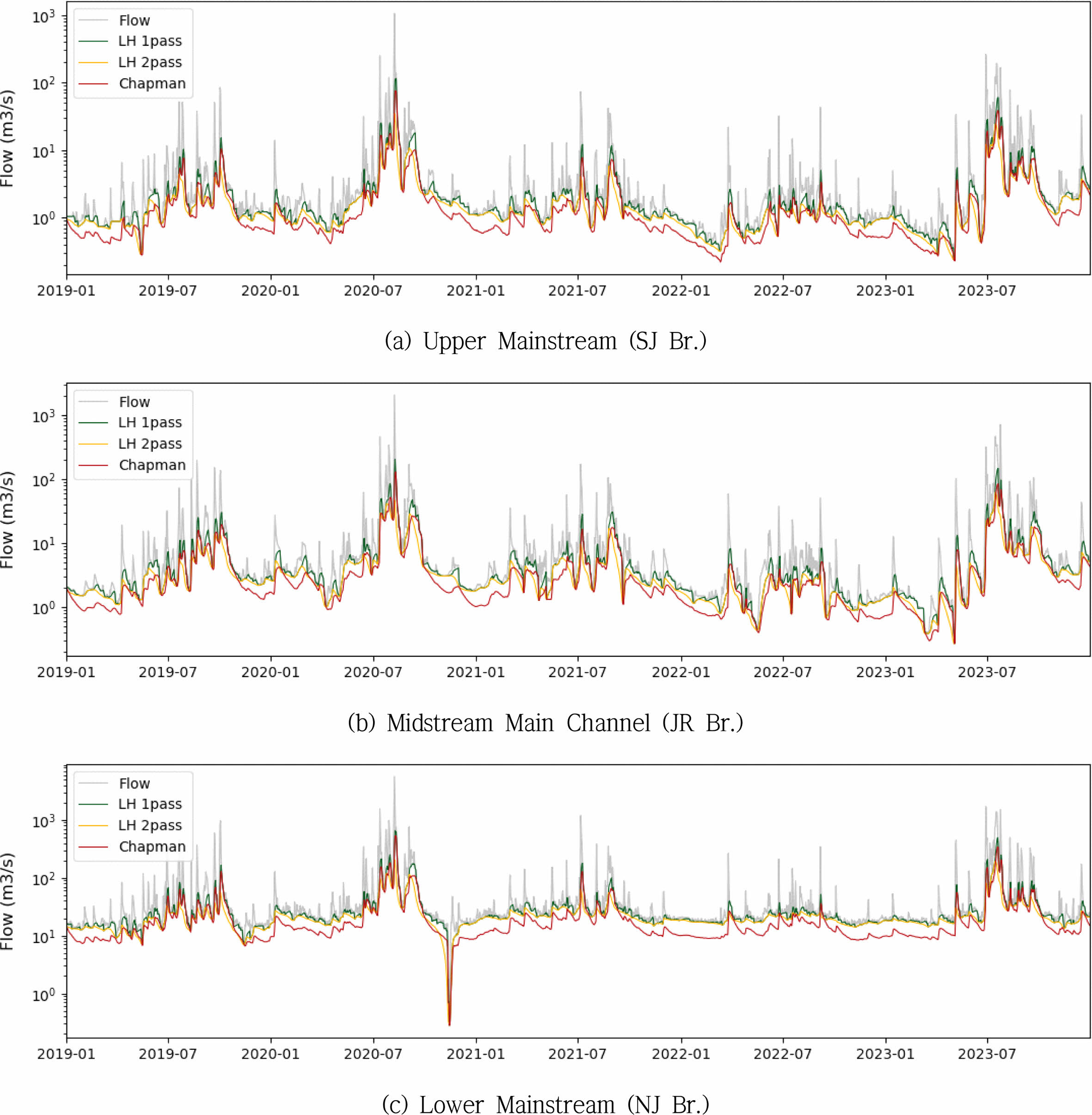
|
Fig. 9 Baseflow estimation results using LH1P, LH2P, chapman methods in the yeongsan watershed. |
|
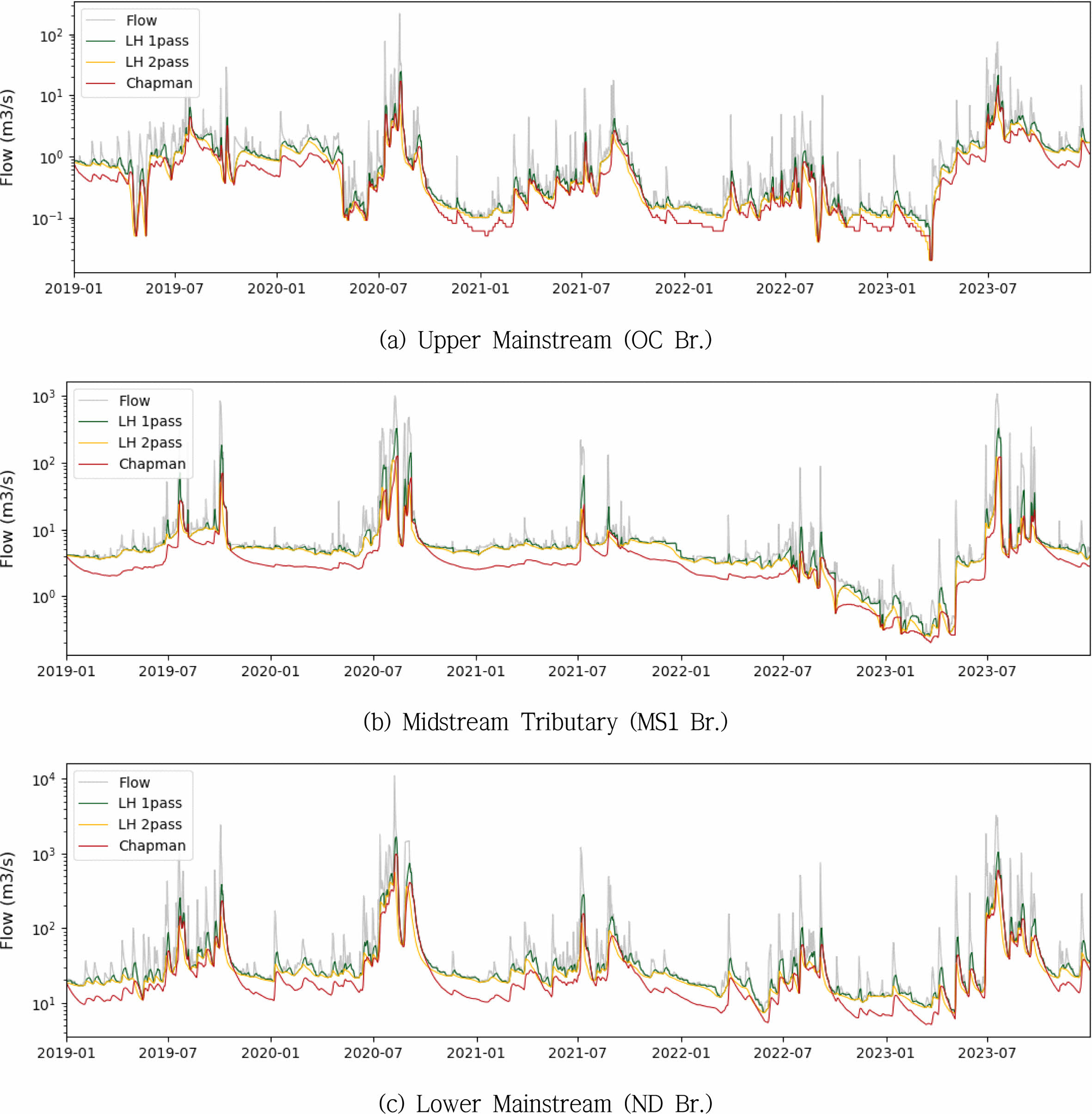
Fig. 10 Baseflow estimation results using LH1P, LH2P, chapman methods in the seomjin watershed. |
|
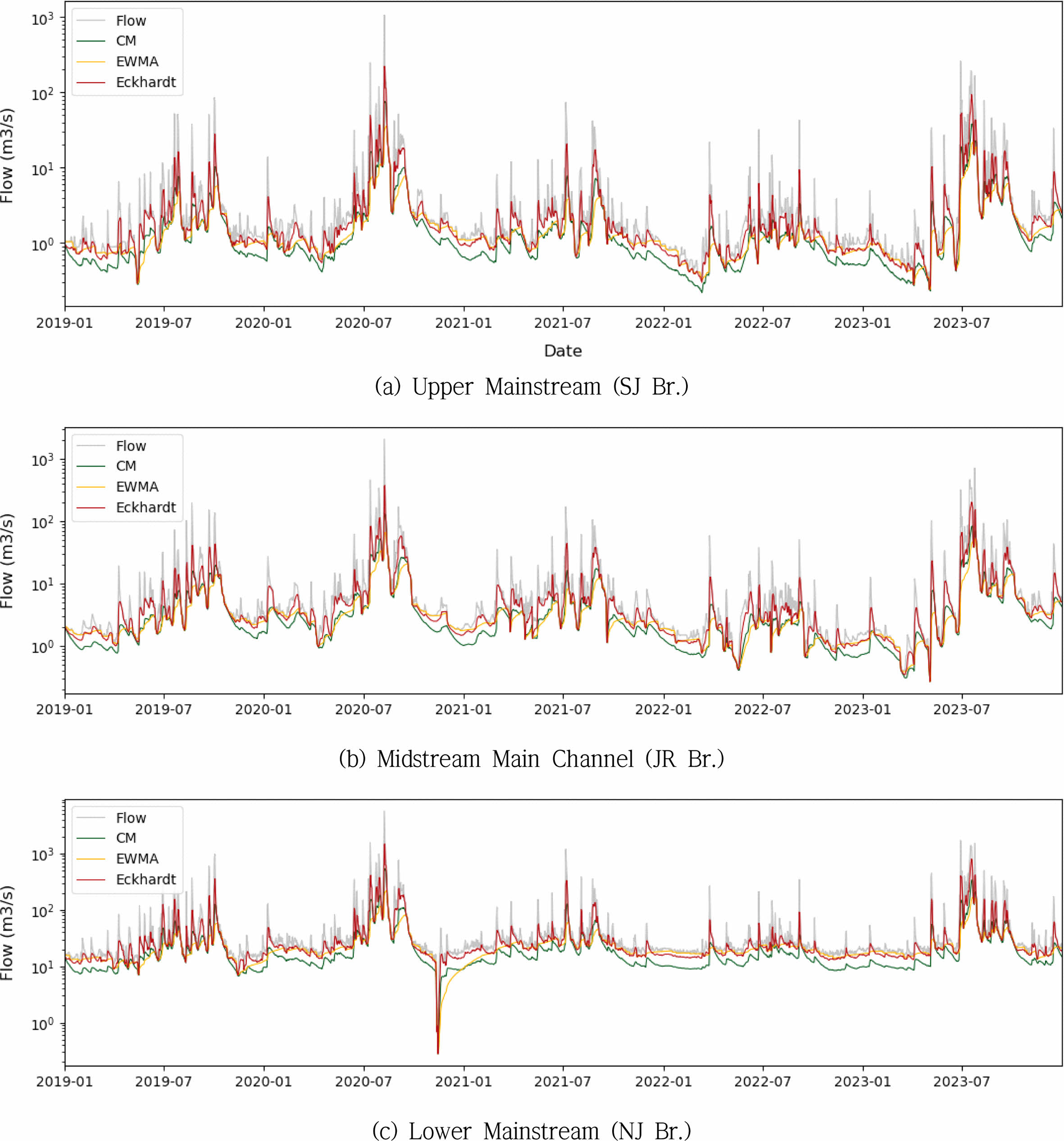
Fig. 11 Baseflow estimation results using CM, eckhardt, and EWMA methods in the youngsan watershed. |
|
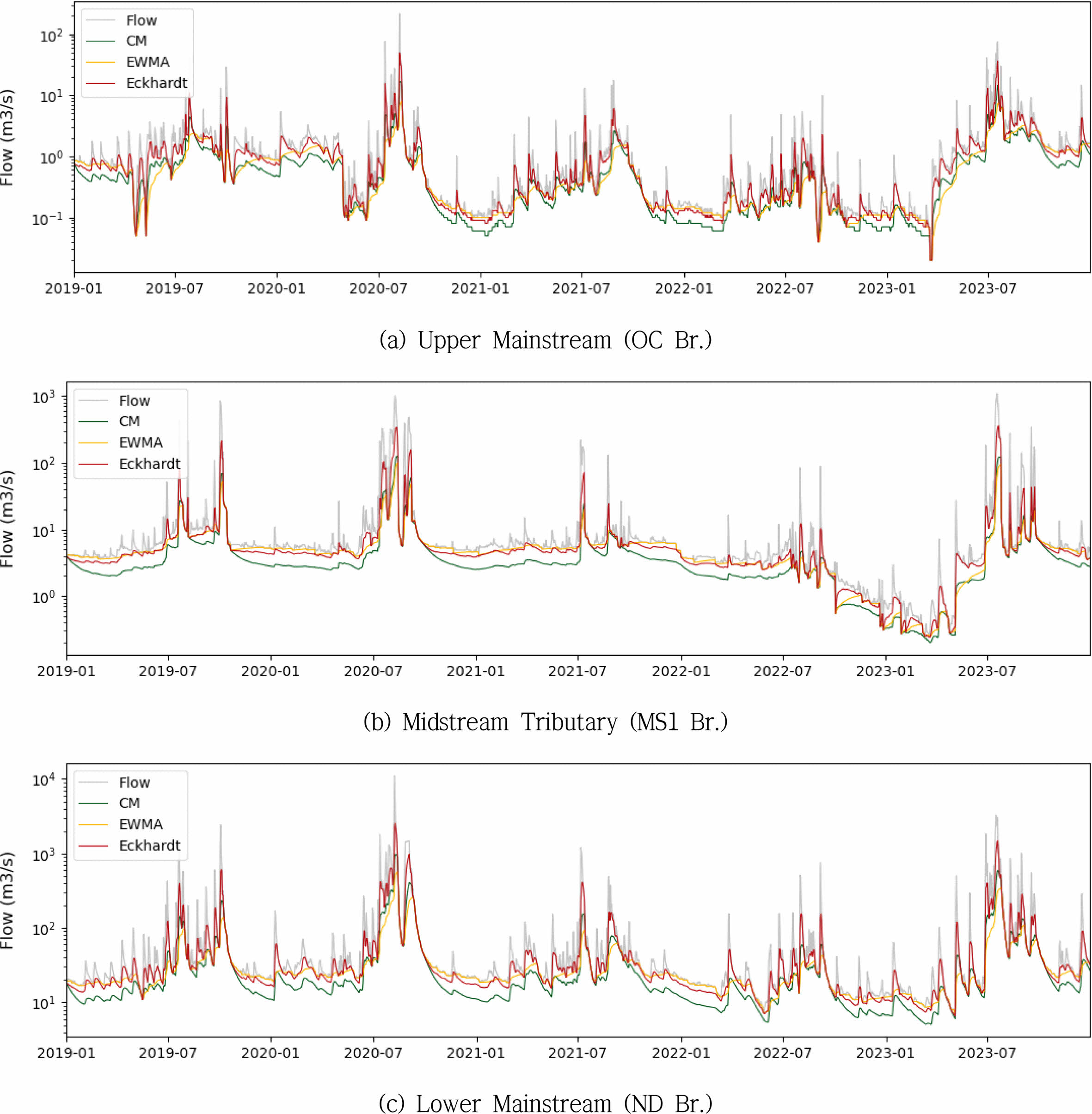
Fig. 12 Baseflow estimation results using CM, eckhardt, and EWMA methods in the seomjin watershed. |
|
Fig. 13 Correlation analysis results of baseflow influencing factors in the mainstreams of the yeongsan and seomjin watersheds. |
|
Fig. 14 Correlation analysis results of baseflow influencing factors in the tributaries of the yeongsan and seomjin watersheds |
|
Table 4 Summary of baseflow index (BFI) results by location using a graphical (Pictorial) method |
|
Table 5 Summary of NSE results by location using a graphical (Pictorial) method |
|
|
Table 6 Changes in baseflow index according to parameter variations by method and monitoring location |
|
Table 8 Results of Correlation Analysis of Baseflow Influencing Factors by Watershed (R2 & t-test) |
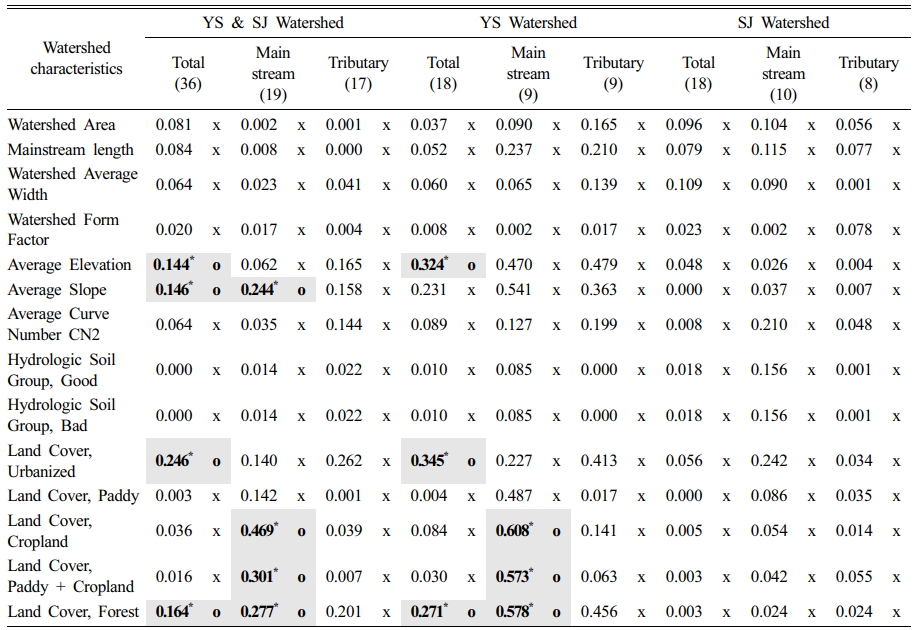
x : 귀무가설 성립(상관관계 없음), O : 귀무가설 기각(상관관계 있음)※ |
본 연구는 영산강 및 섬진강 유역을 대상으로 다양한 기저유출 분리 기법(도식적 방법 및 디지털 필터 방법)을 적용하고, 각 기법의 민감도 및 통계적 적합도를 비교 분석함으로써 유역 특성과 매개변수 변화가 기저유출지수(BFI) 산정에 미치는 영향을 평가하였다. 도식적 방법 중에서는 HYSEP-LMM 방식이 높은 통계적 적합도를 보이며 유역의 수문 반응을 안정적으로 반영하는 것으로 나타났고, 디지털 필터 방법 중에서는 Eckhardt 방법이 NSE, PBIAS, KGE 등의 평가지표에서 우수한 성능을 보이며 최적의 기저유출 분리 기법으로 선정되었다.
총 36개 유량관측 지점에서 산정된 BFI는 유역별·방법별로 다양한 값을 보였으며, 동일 유역 내에서도 분리 방법에 따라 ±0.1 이상의 차이를 나타내는 등 방법론적 민감성이 확인되었다. 이는 단일한 매개변수 설정만으로는 기저유출 특성을 일관되게 반영하기 어려움을 시사하며, 경험적 권장값과 유역 특성에 기반한 매개변수 보정이 병행되어야 함을 보여준다.
또한 GIS 기반의 유역 특성 인자와의 상관분석 결과, 본류 구간에서는 평균 경사, 산림, 농경지 비율이 BFI와 유의한 관계를 보였으나, 지류 및 소규모 유역에서는 단일 변수로 기저유출 변동성을 설명하기에는 한계가 있는 것으로 나타났다. 이는 지하수위, 인공시설 운영, 지질 구조 등 추가적인 요인의 고려가 필요함을 의미한다.
결론적으로, 본 연구는 유역 특성 및 분석 목적에 따라 기저유출 분리 방법을 선별하고, 정량적 평가지표를 활용한 검증 과정을 통해 그 신뢰성과 적용 가능성을 평가하였다는 점에서 의의가 있다. 본 연구 결과는 향후 수문모형 구축, 기후변화 영향 평가, 생태유량 설정, 수질 예측 및 물관리 정책 수립 등에 있어 기저유출 산정의 정량적 기준을 제공할 수 있을 것으로 기대된다. 향후 연구에서는 관측 지하수위 및 기상 정보와의 통합 분석을 통해 기저유출의 시간적·공간적 예측력을 향상시키는 모델링 접근이 요구된다.
본 연구는 영산강·섬진강수계관리위원회 환경기초조사사업의 지원을 받아 수행되었습니다.
- 1. Ahiablame, L., Chaubey, I., Engel, B., Cherkauer, K. and Merwade, V., 2013, Estimation of annual baseflow at ungauged sites in Indiana, USA, J. Hydrol., 476, 13-27.
-

- 2. Aksoy, H., Unal, N. E., and Bavli, H., 2008. Smoothed minima baseflow separation method: Procedure and application, J. Hydrol. Engrg., 13(9), 761-768.
-

- 3. Cey, E.E., Rudolph, D.L., Parkin, G.W. and Aravena, R., 1998, Quantifying groundwater discharge to a small perennial stream in southern Ontario, Canada, J. Hydrol., 210(1-4), 21-37.
-

- 4. Chang, F.J., Huang, C.W., Cheng, S.T. and Chang, L.C., 2017, Conservation of groundwater from over-exploitation—Scientific analyses for groundwater resources management, Sci. Total Environ., 598, 828-838.
-

- 5. Chapman, T. G., 1991, Comment on ¡°Evaluation of automated techniques for base flow and recession analyses¡± by RJ Nathan and TA McMahon. Water Resour. Res., 27(7), 1783-1784.
-

- 6. Chapman, T., 1999, A comparison of algorithms for stream flow recession and baseflow separation, Hydrol. Process., 13(5), 701-714.
-

- 7. Chapman, T.G., and Maxwell, A.I., 1996, Baseflow separation-comparison of numerical methods with tracer experiments, In Institute Engineers Australia National Conference, Institute of Engineers, Canberra, Australia, 5, 539-545.
- 8. Choi, Y.H., Park, Y.S., Ryu, J.C., Lee, D.J., Kim, Y.S., Choi, J.D., and Lim, K.J., 2014, Analysis of baseflow contribution to streamflow at several flow stations, J. Korean Soc. Water Environ., 30(4), 441-451.
-

- 9. Eckhardt, K., 2005, How to construct recursive digital filters for baseflow separation, Hydrol. Process., 19(2), 507-515.
-

- 10. Eckhardt, K., 2012, Analytical sensitivity analysis of a two parameter recursive digital baseflow separation filter, Hydrol. Earth Syst. Sci., 16(2), 451-455.
-

- 11. Gou, S. and Miller, G., 2014, A groundwater–soil–plant–atmosphere continuum approach for modelling water stress, uptake, and hydraulic redistribution in phreatophytic vegetation, Ecohydrology, 7(3), 1029-1041.
-

- 12. Gupta, H. V., Kling, H., Yilmaz, K. K., and Martinez, G. F. 2009, Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modeling. J. Hydrol., 377(1–2), 80–91.
-

- 13. Gustard, A., Bullock, A., and Dixon, J. M., 1992, Low flow estimation in the United Kingdom, Inst. Hydrol, 108, Wallingford, UK.
- 14. Kang, H.S., Hyun, Y.J., and Jun, S.M., 2019, Regional estimation of baseflow index in Korea and analysis of baseflow effects according to urbanization, J. Korea Water Resour. Assoc., 52(2), 97-105.
-

- 15. Kang, T., and Lee, N.j., 2021, Case study on application of graphical method for baseflow separation, J.Korea Water Resour. Assoc., 54(4), 217-227.
-

- 16. Kang, T., Lee, S., Lee, N., and Jin, Y., 2022. Baseflow separation using the digital filter method: review and sensitivity analysis. Water, 14(3), 485.
-

- 17. Kim, J. H., Lee, S. Y., and Lee, S. H., 2020, Baseflow characteristics in agricultural basins under groundwater use pressure. Water, 12(2), 311.
- 18. Knoben, W.J., Freer, J.E. and Woods, R.A., 2019, Inherent benchmark or not? Comparing Nash–Sutcliffe and Kling–Gupta efficiency scores, Hydrol. Earth Syst. Sci., 23(10), 4323-4331.
-

- 19. Ladson, A.R., Brown, R., Neal, B. and Nathan, R., 2013, A standard approach to baseflow separation using the Lyne and Hollick filter, Australasian J. Water Res., 17(1), 25-34.
-

- 20. Lee, S.C., Kim H.Y., Kim H.J., Han J.H., Kim, S.J., Kim, J.G., and Lim, K.J., 2017, Analysis of Baseflow Contribution based on Time-scales Using Various Baseflow Separation Methods, J. Korean Soc. Agric. Eng., 59(2), 1-11.
-

- 21. Lott, D.A. and Stewart, M.T., 2013, A power function method for estimating base flow, Groundwater, 51(3), 442-451.
-

- 22. Lott, D.A. and Stewart, M.T., 2016, Base flow separation: A comparison of analytical and mass balance methods, J. Hydrol., 535, 525-533.
-

- 23. Lyne, V. and Hollick, M., 1979, Stochastic time-variable rainfall-runoff modeling, In Institute of Engineers Australia National Conference,79, 10-89.
- 24. Lyu, Y., Luo, W., Wang, Y., Zeng, G., Wang, Y., Cheng, A., Zhang, L., Chen, J., Cai, X., Zhang, R. and Wang, S., 2020, Impacts of cave ventilation on drip water ¥ä13CDIC and its paleoclimate implication, Quat. Int., 547, 7-21.
-

- 25. Matsubayashi, U., Velasquez, G.T. and Takagi, F., 1993, Hydrograph separation and flow analysis by specific electrical conductance of water, J. Hydrol., 152(1-4), 179-199.
-

- 26. Moriasi, D.N., Arnold, J.G., Van Liew, M.W., Bingner, R.L., Harmel, R.D. and Veith, T.L., 2007, Model evaluation guidelines for systematic quantification of accuracy in watershed simulations, Trans. ASABE., 50(3), 885-900.
-

- 27. Nathan, R.J. and McMahon, T.A., 1990, Evaluation of automated techniques for base flow and recession analyses, Water Resour. Res., 26(7), 1465-1473.
-

- 28. Park, S., Nielsen, A., Bailey, R.T., Trolle, D. and Bieger, K., 2019, A QGIS-based graphical user interface for application and evaluation of SWAT-MODFLOW models, Environ. Modell. Software., 111, 493-497.
-

- 29. Piggott, A.R., Moin, S. and Southam, C., 2005, A revised approach to the UKIH method for the calculation of baseflow/Une approche améliorée de la méthode de l'UKIH pour le calcul de l'écoulement de base, Hydrol. Sci. J., 50(5).
-

- 30. Pilgrim, D.H., Huff, D.D. and Steele, T.D., 1979, Use of specific conductance and contact time relations for separating flow components in storm runoff, Water Resour. Res., 15(2), 329-339.
-

- 31. Pinder, G.F. and Jones, J.F., 1969, Determination of the ground‐water component of peak discharge from the chemistry of total runoff, Water Resour. Res., 5(2), 438-445.
-

- 32. Rutledge, A.T., 1998, Computer programs for describing the recession of ground-water discharge and for estimating mean ground-water recharge and discharge from streamflow records: Update (No. 98), US Department of the Interior, US Geological Survey.
-

- 33. Saraiva Okello, A.M.L., Uhlenbrook, S., Jewitt, G.P., Masih, I., Riddell, E.S. and Van der Zaag, P., 2018, Hydrograph separation using tracers and digital filters to quantify runoff components in a semi‐arid mesoscale catchment, Hydrol. Process., 32(10), 1334-1350.
-

- 34. Sloto, R.A. and Crouse, M.Y., 1996, HYSEP: A computer program for streamflow hydrograph separation and analysis, U.S. Geol. Surv., 96-4040.
-

- 35. Stewart, M., Cimino, J. and Ross, M., 2007, Calibration of base flow separation methods with streamflow conductivity, Groundwater, 45(1), 17-27.
-

- 36. Tularam, G.A., and Ilahee, M., 2008, Exponential smoothing method of baseflow separation and its impact on continuous loss estimates, Am. J. Environ. Sci., 4(2), 136-144.
-

- 37. Xie, J., Liu, X., Wang, K., Yang, T., Liang, K. and Liu, C., 2020, Evaluation of typical methods for baseflow separation in the contiguous United States, J. Hydrol., 583, 124628.
-

- 38. Yang, H., 2006, Runoff characteristics of non-point source pollutants in storm event -Case study on the upstream and downstream of Kokseong River, Korea-, J. Korean Geogr. Soc., 41(4), 418-434.
- 39. Yeongsan River Flood Control Office, www.yeongsanriver.go.kr/sumun/wlList.do?S=S01 [accessed 25.05.29]
- 40. Yu, Z. and Schwartz, F.W., 1999, Automated calibration applied to watershed‐scale flow simulations, Hydrol. Process., 13(2), 191-209.
-

- 41. Zhang, J., Zhang, Y., Song, J. and Cheng, L., 2017, Evaluating relative merits of four baseflow separation methods in Eastern Australia, J. Hydrol., 549, 252-263.
-

- 42. Zhang, Y., Ahiablame, L., Engel, B. and Liu, J., 2013, Regression modeling of baseflow and baseflow index for Michigan, USA, Water, 5(4), 1797-1815.
-

 This Article
This Article
-
2025; 30(3): 29-53
Published on Jun 30, 2025
- 10.7857/JSGE.2025.30.3.029
- Received on May 26, 2025
- Revised on May 29, 2025
- Accepted on Jun 15, 2025
 Services
Services
Shared
 Correspondence to
Correspondence to
- In Kyun Jung
-
국립한밭대학교 건설환경공학과
- E-mail: nemoik@nate.com