- Sensitivity Analysis of Hydrodynamic and Reaction Parameters in Gasoline Transport Conceptual Aquifer Model Based on Hydrogeological Characteristics of Korea
Jin Chul Joo1·Dong Hwi Lee1·Hee Sun Moon2,*·Sun Woo Chang3·Soo-Hyoung Lee2 ·Eunhee Lee2·Kyoungphile Nam4
1Department of Civil and Environmental Engineering, Hanbat National University
2Groundwater Research Center, Korea Institute of Geoscience and Mineral Resources
3Department of Land, Water and Environment Research, Korea Institute of Civil Engineering and Building Technology
4Department of Civil and Environmental Engineering, Seoul National University- 국내 대수층 특성을 반영한 포화대 내 유류오염물질 거동 개념 모델에서 수리동역학적 및 반응 입력인자 민감도 평가
주진철1·이동휘1·문희선2,*·장선우3·이수형2·이은희2·남경필4
1한밭대학교 건설환경공학과
2한국지질자원연구원 지질환경연구본부 지하수연구센터
3한국건설기술연구원 국토보전연구본부
4서울대학교 건설환경공학부
Sensitivity analysis of hydrodynamic and reaction parameters in
conceptual model reflecting aquifer characteristics of Korea was performed to
evaluate the uncertainty in the predicted concentrations. Among the
hydrodynamic input parameters, both hydraulic conductivity (Kx)
and hydraulic gradient (I) affected transport behaviors of contaminants,
and resulted in same convergence concentrations with continuous injections of
contaminant. However, longitudinal dispervisity (αL) affected
both transport behaviors and the convergence concentrations of contaminants.
Compared to the hydrodynamic parameters, growth kinetic and degradation
parameters (μm & Kc) more significantly
affected both transport behaviors and the convergence concentrations of
contaminants, indicating those parameters had higher sensitivity indices
causing the uncertainties of model predictions. Considering that the
sensitivity indices of both hydrodynamic and reaction parameters were a
function of transport distance of groundwater, the parameters with higher
sensitivity indices, a priori, need to be investigated using conceptual
model reflecting site-specific aquifer characteristics before field
investigation. After determining the parameters with higher sensitivity
indices, the detail field investigations for the selected hydrodynamic and
reaction parameters were warranted to reduce the uncertainties of model
predictions.
Keywords: Conceptual model, Groundwater, Hydrodynamic parameter, Reaction parameter, Sensitivity analysis, Uncertainty
일반적으로 지중(subsurface)환경으로 오염물질(conta-
minant)이 유출되는 경우, 유출된 오염물질은 지중 내 다양한 이동 경로(pathway)를 따라 물리적, 화학적, 생물학적 변환(transformation)
등의 복잡한 반응을 통해 희석(dilution) 및 저감(attenuation)된다. 지중환경 내에서 이러한 희석 및 저감 기작을 거치는 동안
오염물질의 존재 형태(speciation), 독성(toxicity), 이동성(mobility) 등은 다양하게 변화해 궁극적으로 인간이나 생태계에
미치는 위해도 또한 달라질 수 있다(Mackay et al., 1985; Clement, 1999; Lapworth et al., 2012; Essaid et al., 2015). 따라서,
오염물질의 지중 내 존재 형태, 이동 경로와 변환에 따른 노출농도(exposure concentration)의 차이는 수용체(receptor)에
미치는 위해성 정도에 큰 영향을 미치며, 타당한 위해성 평가(risk assessment)를 위해서는 지중환경 내 오염원 (source)-이동
경로(pathway)-수용체(receptor) 시스템 내에서 오염물질의 이동(transport)과 반응(reaction) 관련된 다양하고 복잡한
과정 등을 고려하여 노출농도를 결정해야 한다(USEPA, 1996; ASTM, 1999; Kim and Park, 2007; Bailey et
al., 2013).
일반적으로 토양오염부지 위해성평가에서 토양 및 지하수 이동 경로를 통한 수용체(인간)에 대한 오염물질의 노출농도의 결정은 현장 정밀조사를
통한 실측치(measured values) 또는 수학적 모델(mathematical model)을 통한 예측치(predicted values)로
결정할 수 있는 것으로 보고되고 있다(USEPA, 1996; ASTM, 1999; Kim and Park, 2007; Bailey
et al., 2013; Chang et al., 2019). 그러나, 광역적 규모(regional scale)의 오염부지 등의 위해성
평가를 현장조사를 통한 실측치에만 의존해 오염물질의 시간(temporal)과 공간(spatial)에 따른 노출농도를 결정하는 기법은 한계가 있으며,
오염부지 사후관리 시 시공간별 위해성 변화에 따른 오염부지 관리계획 수립 등을 고려 시 수학적 모델을 병행하는 것이 합리적이다.
지중환경 내 오염원−이동 경로−수용체의 시스템에서 오염물질의 시공간별 거동(fate and
transport)을 예측할 수 있는 수학적 모델은 이동과 반응을 비교적 단순화한 1차원 해석모델, 시공간에 따른 이동과 반응의 비균질성을 고려한
다차원의 수학적 모델과 두 모델을 병행한 하이브리드 모델로 구분할 수 있다(USEPA, 1996; ASTM, 1999; Kim and
Park, 2007). 또한, 다양한 입력변수와 실측 자료가 충분한 경우 확정된 입력변수와 부지의 수리지질학적 특성을 통해 오염물질의 거동을 예측하는
확정적(deterministic) 모델과 제한된 입력변수와 실측자료를 대신해 확률 분포화된 입력변수와 수리지질학적 특성을 통해 오염물질의 거동을
예측하는 확률적(stochastic) 모델로 구분할 수 있다(USEPA, 1988; ASTM, 1999; Kim and Park, 2007;
Bailey et al., 2013).
본 연구에서는 포화대 오염물질의 거동(fate and trans-
port)을 예측할 수 있는 수학적 모델로 시공간에 따른 이동과 반응의 비균질성을 고려한 지하수 유동 및 오염물질 거동을 예측하기
위해 3차원 지하수 유동 모델인 MODFLOW(Harbaugh and McDonald, 1988)와 오염물질의 다양한 반응을 모사한
RT3D(Clement, 1999)를 연계하여 활용하였다.
MODFLOW와 RT3D는 유한차분법 모델로서 포화대에서의 지하수 유동 및 오염물질 거동을 예측하는데 널리 활용되고 있다(USEPA,
1996; ASTM, 1999; Bailey et al., 2013).
오염지역의 충적 대수층을 대상으로 지하수 유동 및 오염물질 거동을 예측 시 부지 특성화(site-specific)를 위해 수리동역학적(hydrodynamic)
특성과 물리적, 화학적, 생물학적 반응(reaction)과 관련된 다양한 자료 조사가 현장에서 수행되어야 하나, 현장조사가 불가능한 경우 개념
모델을 설정 시 다양한 입력 변수들의 변화에 따른 민감도 분석을 통해 모델 예측치에 대한 개략적인 불확실성에 대한 선행적인 평가가 요구된다. 따라서, 본 연구에서는
지중환경 내 오염물질의 이동 경로에 따른 노출농도를 결정하기 위해서는 우리나라 지중환경을 모사한 개념 모델을 구축 후 국내 대수층 특성에
적합한 수리동역학적 변수[투수계수(Kx), 수리학적 구배(I), 유효 공극률(n),
종분산계수(αL)]와 반응 변수[수착(Kd)과 생분해(μm
& Kc)]를 활용해 오염물질의 포화대 내 시공간적 거동을 예측하였으며, 이러한 수리동역학적 변수와 반응 변수의
변화가 오염물질의 거동에 미치는 영향을 예측하여 민감도 분석을 통해 다양한 입력변수의 변화에 따른 모델 예측치의 변화를
시공간에 따라 정량화하였다. 이를 통해 위해성 평가 시 활용하는 3차원 지하수 모델인 MODFLOW-RT3D 모델 예측치에 영향을
미치는 입력변수들 사이의 상대적 민감도를 확인할 수 있으며, 개념 모델 수립 및 모델 보정 과정에서 모델의 불확실성을 선행적으로 평가 후 부지
특성화를 위한 현장조사 자료를 보완해 불확실성 문제를 저감시킬 수 있다.
본 연구의 주요 목표는 우리나라 대수층을 대표하는 개념 모델(conceptual model)을 바탕으로 수치모델을 개발하여 지하수 유동과
오염물질 거동을 예측 시 국내 대수층 특성에 적합한 수리동역학적 변수(투수계수, 수리학적 구배, 유효공극률, 분산)와 반응 변수(수착, 분해)의
민감도 분석을 통해 입력변수의 변화에 따른 모델 예측치의 불확실성을 조사하는 것이다. 주요 세부 목표로는 (1) 수리동역학적 변수 변화에 따른
비반응성 물질의 거동을 조사하고, (2) 반응 변수 변화에 따른 반응성 물질의 거동을 조사하며, (3) 모델 입력변수들의 변화에 따른 농도차의
시공간적 분석과 민감도를 분석하는 것이다.
2.1. 지배방정식(Governing Equation)
포화대에서의 3차원 지하수 유동 지배방정식은 질량보전의 법칙을 이용해 산출되며, 불균일(heterogeneous)하고 이방성(anisotropic)인
대수층이며, 지하수계로 유입/유출되는 단위 체적당유량을 고려할 경우, 식 (1)과 같이 제시할 수 있다(Fetter, 2001).
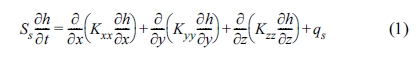
여기에서 Ss는 비저류계수(1/T), h는 수두(L), t는 시간(T), K는 투수계수(L/T), qs는
지하수계로 유입/유출되는 단위 체적당 유량(1/T)을 의미하며, x, y, z는 데카르트 좌표이다.
대수층 내에서 지하수의 유동에 따른 이류(advection)와 분산(dispersion)의 수리동역학적 과정 이외에 선형 수착(sorption)과
미생물에 의한 생물학적 분해(degradation)를 고려한 대수층 내 각각의 오염물질의 이동 지연(retardation) 및 농도 저감(attenuation)은
식 (2)와 같은 이류-분산-반응(advection-dispersion-reaction equation)의 지배방정식으로 나타낼 수 있다. 특별히
식(2)에서는 미생물의 성장속도(growth kinetics)를 고려한 오염물질의 생분해를 Double monod kinetics를 활용해 제시하였으며,
미생물의 성장속도는 전자공여체(electron donor)인 오염물질과 전자수용체(electron acceptor)인 용존산소 농도에 따라 결정되며
이를 통해 지하수 내 오염물질의 시공간에 따른 농도가 결정된다.
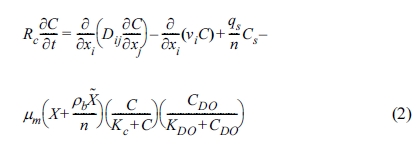
여기에서 i, j는 벡터 성분이며, C는 지하수 내 오염물질 농도(M/L3), Cs는
유입 오염원에서 오염물질 농도(M/L3), CDO는 지하수 내 용존산소 농도(M/L3),
X는 지하수 내 미생물 농도(M/L3), ![]() 는 토양에 부착된 미생물 농도(M/M), x는 지하수의 이동거리(L),
Rc는 오염물질 지연계수(dimensionless), D는 기계적 분산(Dm)과
분자확산(D*)이 고려된 수리동역학적 분산(L2/T), v는 지하수 유속(L/T),
n은 유효공극률(dimensionless), μm은 미생물의 최대 오염물질 섭취율(1/T), ρb는
겉보기 밀도(M/L3), Kc는 오염물질 반포화 상수(M/L3), KDO는
용존산소 반포화 상수(M/L3)로 정의된다.
는 토양에 부착된 미생물 농도(M/M), x는 지하수의 이동거리(L),
Rc는 오염물질 지연계수(dimensionless), D는 기계적 분산(Dm)과
분자확산(D*)이 고려된 수리동역학적 분산(L2/T), v는 지하수 유속(L/T),
n은 유효공극률(dimensionless), μm은 미생물의 최대 오염물질 섭취율(1/T), ρb는
겉보기 밀도(M/L3), Kc는 오염물질 반포화 상수(M/L3), KDO는
용존산소 반포화 상수(M/L3)로 정의된다.
또한, 전자 수용체(electron acceptor)인 용존산소(dis- solved oxygen), 지하수 내 부유미생물(suspended
micro-
organisms), 토양에 부착된 미생물(attached micro- organisms)의 이류-분산-반응의 지배방정식은 각각
식(3), 식(4), 식(5)에 제시되었다. 이러한 지배방정식을 기반으로 3개의 이동상 물질(오염물질, 용존산소, 지하수 내 미생물)이 지하수의 유동과 동시에
지중환경과의 다양한 반응(수착, 생분해, 미생물의 성장/사멸/부착/탈착 등)을 모사할 수 있으며, 1개의 고정상 물질(토양 부착 미생물)의 성장/사멸/부착/탈착을
모사할 수 있다.
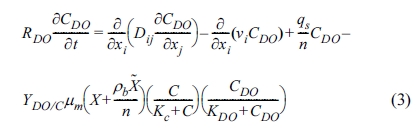
여기에서 RDO는 용존산소 지연계수(dimensionless)이며, YDO/C는
오염물질의 분해 시 소요되는 용존산소의 화학양론 수율계수(dimensionless)로 정의된다.
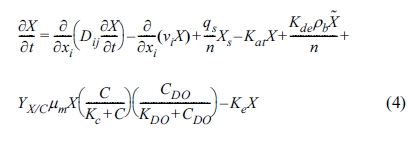
여기에서 Xs는 유입 오염원에서 미생물 농도(M/L3), Kat는
지하수에서 토양으로 미생물의 부착계수(1/T), Kde는 토양에서 지하수로 미생물의 탈착계수(1/T), Ke는
지하수 내 미생물의 사멸계수(1/T), YX/C는 오염물질 분해 시 성장하는 미생물의 화학양론 수율계수(dimensionless)로
정의된다.
또한, 토양에 부착된 미생물의 성장은 식(5)와 같은 미분방정식을 활용해 예측할 수 있으며, 부착성 미생물의 성장은 Baveye
and Valocchi(1989)가 제시한 거시적 모델(macroscopic model)을 활용했으며, 부착성 미생물의 성장으로 인한 공극과 침투율의
변화는 미미한 것으로 가정하여 고려하지 않았다.
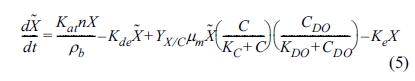
반응-연산 분할전략(reaction-operator splitting strategy)을 통해서 3개의 이동상 물질(오염물질, 용존산소,
지하수 내 미생물)과 1개의 고정상 물질(토양 부착 미생물)의 거동을 지하수의 시공간적 유동과 동시에 4개 물질의 반응 미분식을 음함수 기법(implicit
scheme)으로 산출할 수 있다(Clement, 1999; Clement et
al., 1998).
2.2. 3차원 개념모델(Conceptual
model) 설정
본 연구에서는 이류-분산-반응(advection-dispersion-reaction equation)의 지배방정식에 활용되는 다양한
입력변수의 민감도 분석을 위해 3차원의 대수층 개념모델을 구축하였으며, 지하수 내 오염물질의 시공간적 거동을 모사하기 위해
MODFLOW(McDonald and Harbaugh, 1988)와 RT3D(Clement, 1999)를 연계해 활용하였다. 국내 유류오염 지역 12지역 시추조사 67개 자료를 수집하여 수리지질특성을 통계적으로 분석한 결과, 충적대수층
포화대 구간은 주로 sandy loam으로 조사되었으며, 최대 두께가 약 10 m 내외로 분포되는 것으로
확인되었다. 따라서 국내 유류오염 지역의 지중환경 특성과 오염지역 영향반경을 고려해 본 연구에서 설정한 개념모델은 Fig. 1에 제시된 것처럼,
3차원의 모델 도메인으로 가로(x) 500 m, 세로(y)
300 m, 높이(z) 11 m로 설정하였으며, 모델
격자는 가로 100개, 세로 60개, 높이 2개로 구축해 5 m 간격의 모든 격자에서
시공간에 따른 오염물질의 농도를 예측할 수 있다.
모델 구동 시 도메인의 좌측 경계(x=0 m)는 높은 고정 수두(H=10 m)를 우측 경계(x=500 m)는 낮은 고정 수두(H=5 m)를 기본 경계조건으로
설정하고, 좌측 경계에서 우측 경계로 지하수의 유동이 발생하며, 이외의 모델 도메인 경계는 무흐름(no flow) 경계로 설정하였다. 비록 우리나라
충적 대수층을 대상으로 지하수의 개념모델을 설정 시 하부 암반을 통한 지하수 유동을 고려(Na et al., 2007)하거나 타당한 경계조건 설정
선행(Chang et al., 2019)이 개념모델의 불확실성을 감소시킬 수 있으나, 본 연구에서는 국내 유류오염 지역의 지중환경 특성을 고려해
하부 암반 경계조건 및 하천 지류들의 경계조건을 고려하지 않았으며, 기본적인 좌우 경계면에서 수리학적 구배(hydraulic gradient,
I)를 0.01로 유지하였으며, 경계에서는 흐름이 발생하지 않는 비활성화(inactive) 격자로 설정하였다.
본 연구에서 고려한 유류오염물질은 다른 석유계 화합물 대비 물에 대한 용해도가 비교적 높아 지하수 내 오염확산 정도가 큰
BTEX(Benzene, Toluene, Ethylbenzene, Xylene) 중 발암성과 검출빈도가 높은 벤젠(Benzene,
BZ)을 대상으로 하였다. 민감도 분석을 위한 투수계수(Kx), 수리학적 구배(I), 유효공극률(n), 종분산계수(αL)
등의 입력변수 변화에 따른 도메인 내 오염운(plume)의 분포와 확산을 고려해 오염물질의 주입은 주입정(injection well)을 활용해
유량(Qs)을 5 m3/d로
설정하였으며, 지속적으로 주입한 결과 전체 모델 도메인 내 지하수 유동량의 20%로 분석되었다. 또한, 주입정에서 BZ의 유입농도(Cs)는
수착과 생분해를 통한 BZ의 질량 변화를 검토하기 위해 저농도(Cs=1 mg/L)로 설정하여 주입되는
BZ 질량이 수착과 생분해를 통해 변화 시 발생하는 BZ 농도 변화를 용이하게 관측할 수 있도록 설정하였다(Fig. 1).
BZ의 주입에 따른 모델 대수층 내 오염물질의 거동을 확인하고자 깊이(z) 5 m의 관측정(observation
wells)을 주입정에서 10 m 간격으로 100 m까지 구축하여 BZ의 시간대별
농도 변화를 확인하였으며, 일부 오염운은 10,000일이 경과 후 관측정의 범위를 넘어서 이동 및 확산하므로 추가로 150, 200 m에 관측정을 설치하였다.
이러한 관측정 내의 BZ 농도 변화를 시간에 따라 관측하거나 동일시간에 지하수 이동 거리에 따른 BZ 농도 변화를 관측하여 지하수 내 BZ 거동을
예측해 수리동역학적 변수와 반응 변수들의 민감도(sensitivity)를 분석하였다.
2.3. 수리동역학적 변수와 반응
변수들의 민감도(sensitivity) 분석
민감도 분석은 모델 입력변수 변화에 의해 모델 예측치가 얼마나 변하는지를 분석하는 방법으로, 모델 입력변수들로 인한 모델 예측치의 불확실성을
정량적으로 평가하여 모델을 활용한 예측 시 의사결정에 반영하게 된다(Song et al., 2015). 모델 대수층 내 BZ 이동(transport)에
주요한 영향을 미치는 수리동역학적 변수로는 투수계수, 수리학적 구배, 유효공극률, 종분산계수를 도출하였으며, BZ 반응(reaction)에 주요한
영향을 미치는 반응 변수로는 수착(Kd)과 생분해(μm & Kc)를
도출하였다. 입력된 변수들의 수리동역학적 변수들의 값의 범위는 국내 유류오염 지역의 대수층 조건에서 관측되는 범위의 값을 주로 설정하였으며, 일부
범위의 값은 민감도 분석을 위해 문헌을 참고해 임의로 설정하였다(Fetter, 2001; Han, 2015). 투수계수(Kx)는
silt에서 clean sand의 다공질 매질이 갖는 범위인 0.00864~0.864 m/d의 범위 내에서 10배씩 값을 변화시켰고, 수리학적 구배(I)와 유효공극률(n)은
silt와 clean sand의 매질에서 주로 관찰되는 값의 범위 내에서 설정하였다(Fetter, 2001; Han, 2015). 종분산계수(αL)는
대수층 매질의 불균질한 정도와 이동 거리에 따라 오염물질 분포에 큰 영향을 미치는 변수로 일반적으로 지하수 유동 거리의 0.1배로 나타내며(Gelhar
et al., 1992), 이를 고려해 본 연구에서는 모델 도메인의 크기, 모델 격자크기, 투수계수 범위를 고려해 10, 50, 100 m로 설정하였다. 또한,
수리동역학적 변수가 각각 Kx=0.864 m/d, I=0.01,
n=0.4, αL=50일 때 기본 사례(base case)로 설정하고 입력변수의 변화에 따른 모델
예측 농도를 상호 비교하여 민감도를 평가하였다. 또한, 모델 대수층의 x축과 y축 방향으로 균질한 등방성 매체(homogeneous
& isotropic medium)로 정의해 Kx=Ky로
가정한 반면, 흐름방향 (x축과 z축)에 대해 조사하기 위해 z축 방향의 Kz는
Kx값의 0.1로 설정하였으며, 횡분산계수(αT)와 수직분산계수(αV)는
종분산계수(αL)의 0.1과 0.01로 각각 설정하였다.
대수층 내 복잡한 토양 구성성분에서 BZ 수착을 다성분 수착모델을 활용해 예측하는 것이 비실용적이며, 지하수 내 검출되는 대부분의
BZ 농도는 용해도 대비 5~ 10% 미만으로 조사되어
선형 수착(linear sorption) 모형을 따르는 것으로 조사되었다(Joo et al., 2008; 2011; 2012). 또한, 대부분의
비극성 유기오염물질은 낮은 농도에서 경쟁 수착을 나타내지 않으므로 혼합 유기오염물질의 수착도 선형모형으로 설명하는 것이 비교적 타당하다(Joo
et al., 2008; 2011; 2012). 따라서, 본 연구에서는 모델 대수층 내 BZ 거동(fate)에 주요한 영향을 미치는 반응 변수
중 수착은 기존 문헌에서 보고된 유기탄소기반 수착계수(Koc)를 활용하였으며(Delle site, 2001),
국내 대부분의 충적 대수층 내 유기탄소함량( foc)이 0.1% 미만임을 고려해
Koc 값을 최소 13.8, 평균 61.7, 최대 109.6 L/kg-OC을 활용해 비경쟁 선형 수착(noncompetitive
& linear sorption)으로 모의하였다.
비록 다양한 환경조건에 따라 미생물의 성장속도 및 BZ 생분해 속도가 달라지는 것으로 보고되고 있으나(Trigueros et
al., 2010), 용존산소를 전자수용체로 활용 시 비교적 미생물의 활성도가 높으며, 이러한 경우 미생물의 성장 및 BZ
생분해를 Double monod kinetics를 활용해 모사할 수 있는 것으로 보고되고 있다(Chen et al., 1992; Oh et
al., 1994; Clement, 1999; 1998;
Trigueros et al., 2010). 따라서, 본 연구에서는 BZ 생분해는 일부 문헌(Chen et al., 1992; Oh et
al., 1994; Clement, 1998; 1999; Trigueros et al., 2010)을 활용해 Double monod
kinetics의 미생물 성장계수(μm & Kc)와 오염물질 분해 시 성장하는 미생물의
화학양론 수율계수(YX/C)를 도출하여 사용하였다. 본 연구에서 민감도 분석에 활용된 수리동역학적 변수와
반응 변수의 값은 Table 1에 각 사례별로 제시되었다.
모델 대수층 내 오염물질 거동 모의는 MODFLOW를 통해 지하수의 정상류 분포를 모의한 후 지하수위와 유속 분포가 수렴이 된 후 실시하였다.
지하수위와 유속분포가 결정된 후 다양한 수리동역학적 변수와 반응 변수의 변화에 따른 오염물질 거동은 모의 시간 간격을 5일 단위로 365일(1년),
3650일(10년), 10,000일까지 분석하였으며, 오염원과 거리 변화에 따른 농도 변화를 분석하였다. 또한, 다양한 수리동역학적 및 반응 변수의
변화에 따른 오염물질의 거동은 오염원 주입정에서 10 m와 50 m 떨어진 관측정에서 시간에
따른 오염물질의 농도변화를 주로 분석하였다.
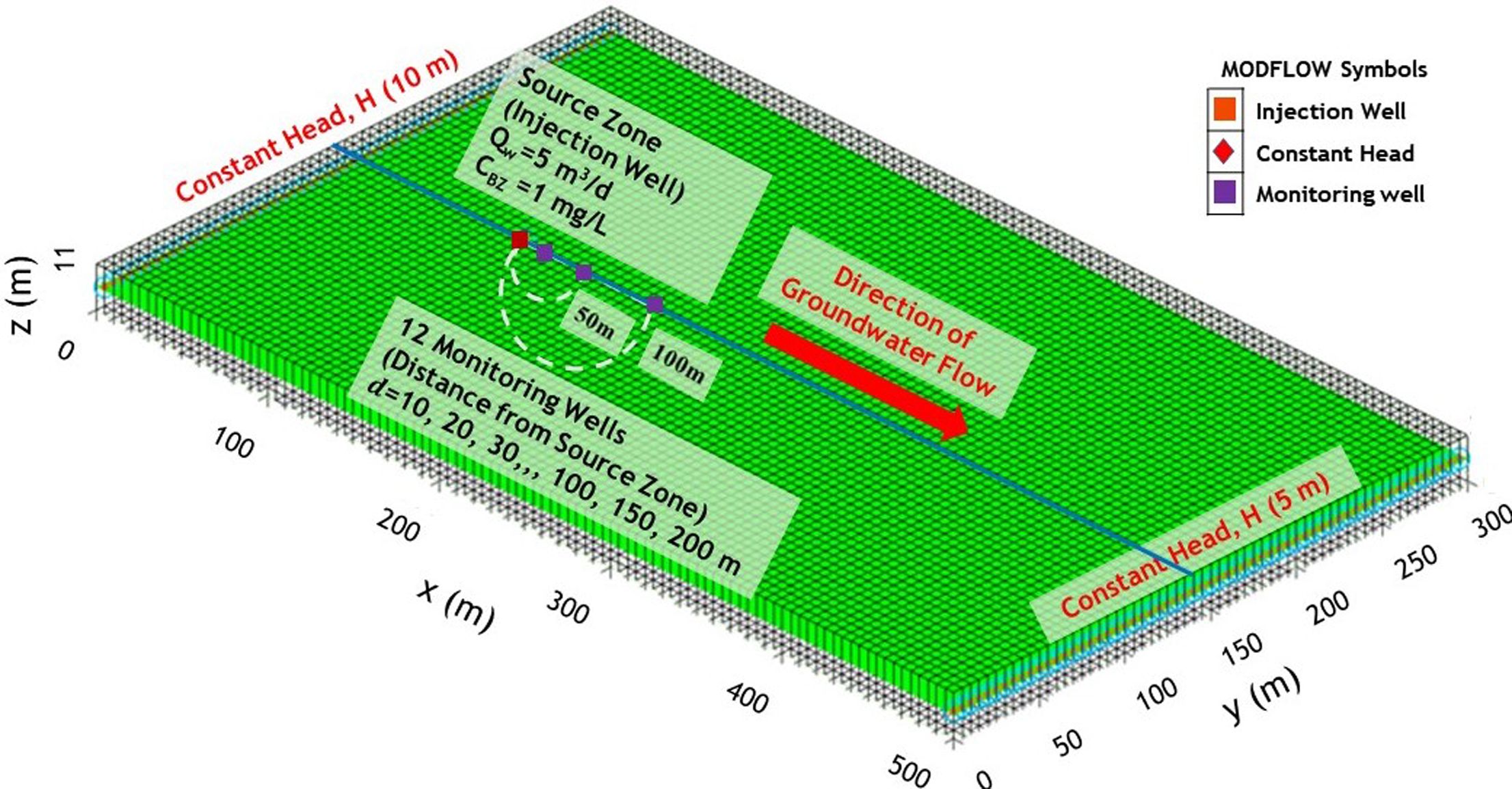
|
Fig. 1 Schematic diagram of conceptual model domain for fate and transport of benzene (BZ) in groundwater flow. |
|
Table 1 Summary of hydrodynamic and reaction parameters for fate and transport of benzene (BZ) for sensitivity analysis |
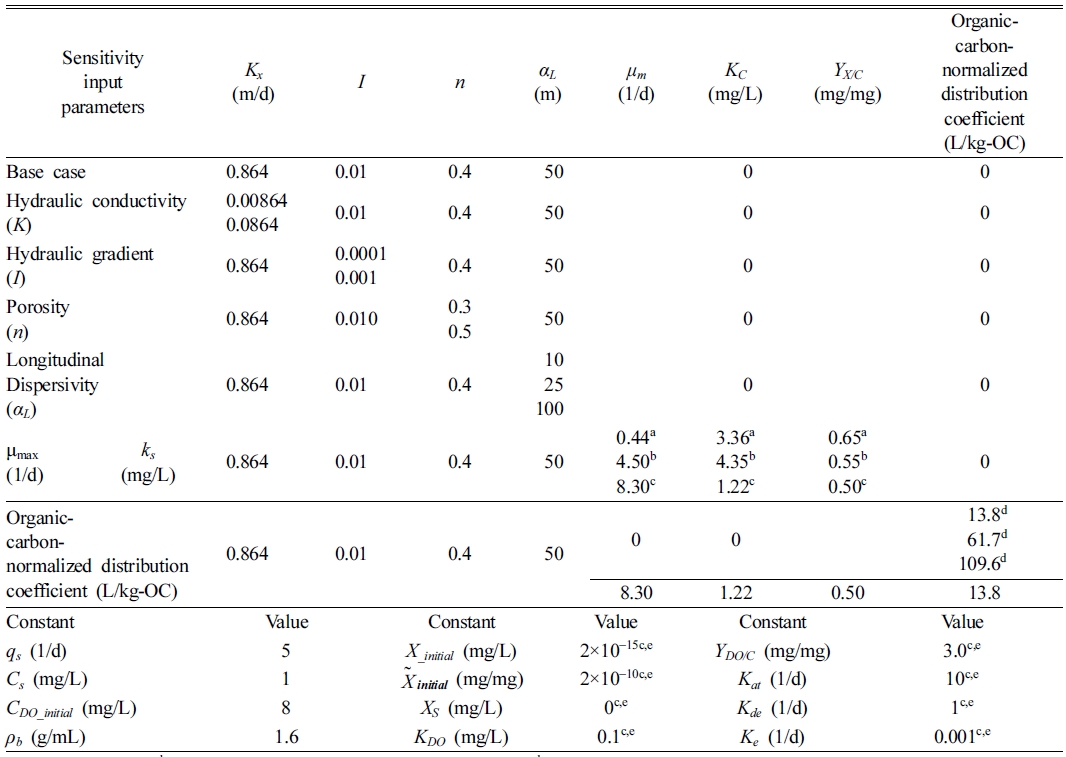
aOh et al. (1994); bTrigueros et al. (2010); cChen et al. (1992); dDelle site (2001); eClement (1999) |
3.1. 기본 사례(base
case)에서 비반응성 물질의 거동
정상상태일 때, 수평 단면 (z=5 m)에서의 지하수의 수두
분포는 Fig. 2(a)에 제시되었으며, 설정된 지하수위 경계조건과 주입정의 지속적인 유입량에 의해 좌측에서 우측으로 갈수록 수위가 점진적으로
감소하는 것으로 조사되었으며, 주입정에서 일부 지하수위 상승이 있으나 다른 대수층 지역에서는 비교적 선형의 지하수위 감소를 나타냈다. 기본 사례의
경우, 지하수 유동방향으로 이류와 수리동역학적 분산이 발생해 10,000일이 경과 후 비반응성 물질의 오염운은 Fig. 2(b)에 제시되었다.
기본 사례의 투수계수와 수리학적 구배 조건에서 물리적/기계적 분산(mechanical dispersion)이 분자 확산(molecular
diffusion) 대비 지배적이며, micro-scale 공극에서 지하수 유속의 차이에 의한 혼합(mixing)으로 인해 주입정에서 비교적 고농도인
오염물질은 이송 및 확산되어 10,000일이 경과 후 오염운의 전면은 모델 도메인의 우측 경계인 500 m까지 이동하였고 희석을
통해 비반응성 물질의 농도는 매우 낮아졌음을 확인할 수 있다.
3.2. 수리동역학적 변수 변화에 따른
비반응성 물질의 거동
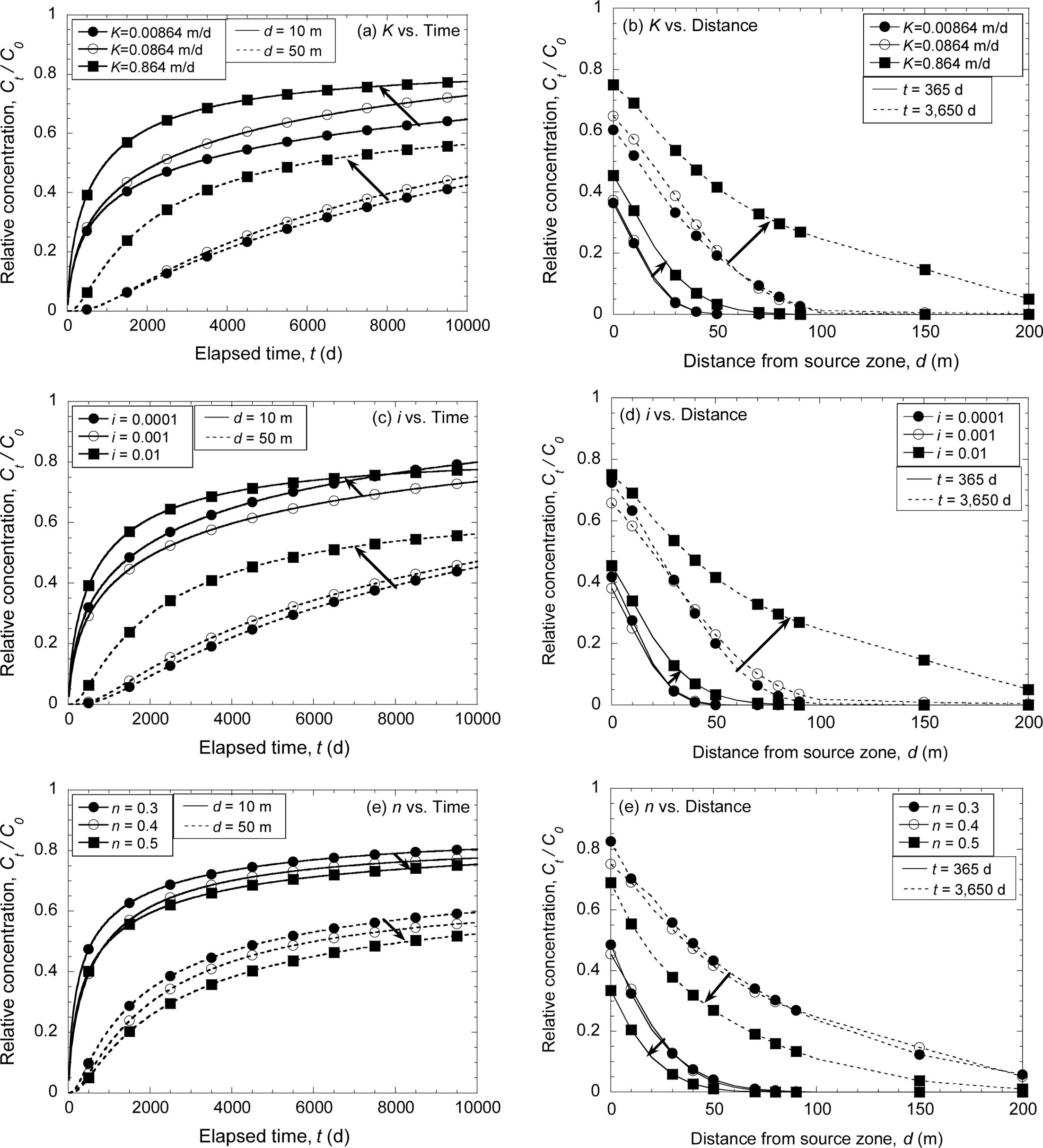
투수계수(Kx)는 지하수 유동에 영향을 주는 인자로서, 투수계수 변화에 따른 비반응성 물질의 시공간에
따른 농도 변화는 Fig. 3(a)와 3(b)에 제시되었다. 투수계수가 증가함에 따라 비교적 빠른 시간에 수렴 농도에 도달하며, 오염원에서 근거리(d=10 m) 보다는 원거리(d=50 m)에서 투수계수 변화에
따른 비반응성 물질의 농도차가 비교적 크게 발생하는 것을 알 수 있다. 또한, 0.00864 m/d에서 0.0864 m/d로 증가 시 오염원에서
원거리에서 농도변화가 미미하지만, 0.0864 m/d에서 0.864 m/d로 증가 시 농도변화가
비교적 큰 것으로 조사되었다. 즉, 투수계수가 0.0864 m/d에서 0.864 m/d로 증가하는 경우,
이류에 따른 비반응성 물질의 이송이 크게 증대되어 지하수 유동 방향에 따른 수리동역학적 분산이 촉진되어 오염운의 이동거리와 농도가 크게 증가하는
것으로 예측되었다.
수리학적 구배(I) 또한 지하수 유동에 영향을 주는 인자로서, 수리학적 구배가 증가함에 따라 지하수 유속이 증가하므로,
오염물질은 보다 원거리까지 이동하게 된다. 수리학적 구배 변화에 따른 비반응성 물질의 시공간에 따른 농도 변화는 Fig. 3(c)와 3(d)에
제시되었으며, 수리학적 구배가 증가 시 지하수 유속이 증가하므로 비반응성 물질의 이송과 분산이 증가함을 확인할 수 있다. 투수계수 변화와 유사하게
수리학적 구배 변화는 오염원에서 근거리(d=10 m) 보다는 원거리(d=50 m)에서 그리고 장기간 지속될
경우 비교적 농도차가 많이 발생하게 된다. 따라서, 투수계수와 수리학적 구배는 지하수의 유속에 큰 영향을 미치며 이로 인해 오염운의 이동거리와
확산범위를 결정함을 알 수 있다.
유효공극률(n) 또한 지하수의 유동에 영향을 주는 인자로서, 유효공극률이 감소함에 따라 동일 유량이 매질을 통과 시 지하수
유속은 증가하므로, 비반응성 물질은 보다 원거리까지 이동 및 확산하게 된다. 유효공극률의 변화에 따른 비반응성 물질의 시공간에 따른 농도 변화는
Fig. 3(e)와 3(f)에 제시되었으며, 유효공극률이 감소 시 지하수의 유속이 증가하므로 비반응성 물질의 이송이 증대되어 상대 노출농도가 일부
증가함을 확인할 수 있다. 그러나, 공극율의 변화가 투수계수와 수리학적 구배의 변화 대비 오염운의 이동과 농도 변화에 미치는 영향이 크지 않은
것으로 조사되었다.
한편, 유효공극률과 투수계수 등은 상호 연관성을 가지고 있어 입력변수들이 상호독립적이라는 민감도 분석의 일반적인 가정(Kim and
Park, 2007)에 부적합하나, 상호독립적이라는 가정하에 수행된 본 민감도 분석결과에서는 투수계수와 수리학적 구배의 변화가 유효공극률의 변화보다는
모델 예측농도에 미치는 불확실성이 상대적으로 큰 것으로 나타났으며, 이는 현장조사 시 투수계수와 수리학적 구배 변수를 부지특성에 타당하게 신중히
결정할 필요가 있음을 의미한다.
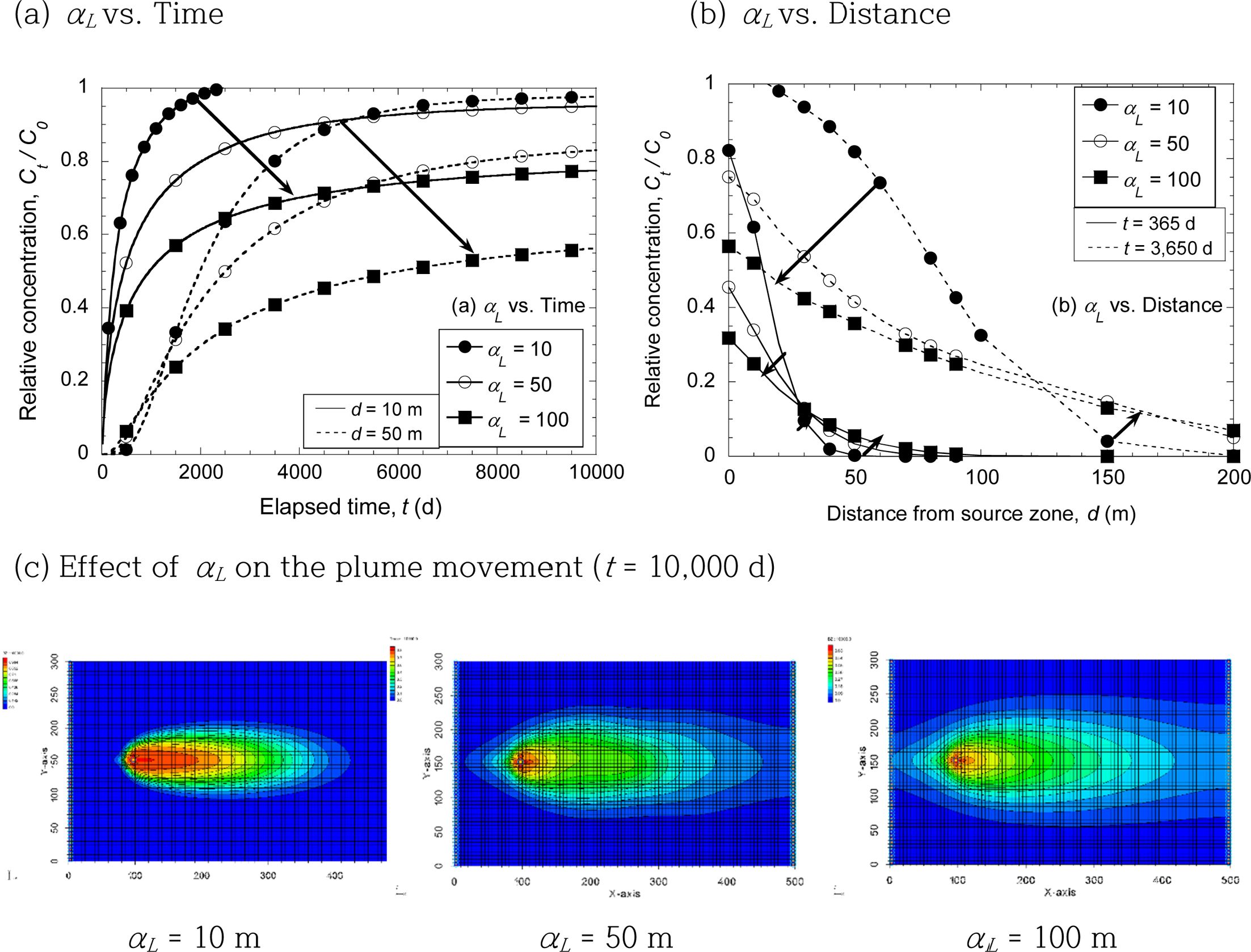
종분산계수(αL)의 변화에 따른 비반응성 물질의 시공간에 따른 농도 변화는 Fig. 4(a)와
4(b)에 제시되었으며, 10,000일이 경과 후 모델 도메인 내 오염운의 변화는 Fig. 4(c)에 제시되었다.
Fig. 4에 제시된 것처럼 분산계수가 증가 시 수리동역학적 분산에 의한 비반응성 물질의 확산이 증대되어 오염물질의 이동 거리는 증대되나 확산에
의한 농도 희석으로 낮은 농도로 수렴함을 알 수 있다. 따라서, 수리동역학적 변수 중 투수계수, 수리학적 구배와 유효공극률은 변수 값이 변화함에
따라 오염물질이 특정 관측점에 도달하는 시간에 영향을 미치나, 장기간 오염물질이 주입 시 수렴 농도 값은 모두 동일한 반면, 종분산계수는 변수
값이 변화함에 따라 오염물질이 특정 관측점에 도달하는 시간에 영향을 미침과 동시에 수렴 농도 값이 크게 차이가 발생함을 알 수 있다(Fig.
4(a)). 즉, 종분산계수가 감소 시 오염운의 확산 범위는 감소하나 오염운 내의 농도가 증가하는 반면, 종분산계수가 증가 시 오염운의 확산 범위는 증대되나
확산에 의한 농도 희석 때문에 오염운 내의 농도는 감소하게 된다(Chang et al., 2019).
본 연구결과와 동일하게 종분산계수(αL)는 지하수 내 오염운의 형태를 결정하는 주요 인자로 보고되고
있으며(Fetter, 1999; Zheng and Gorden, 2002), 지하수 내 오염물질 및 열 거동과 관련된 민감도 분석 시 비교적 민감도가
큰 변수로 평가되고 있다(Atlabachew et al., 2013; Park et al., 2015; Chang et al., 2019). 본
연구에서 설정한 균질한 모델 도메인에서 수리동역학적 변수 중 종분산계수의 변화가 모델 예측농도에 미치는 불확실성이 가장 큰 것으로 조사되어, 실제
현장 부지에서는 미세 공극(micro-scale)에서 대수층 크기(mega-scale)까지의 불균질성(heterogeneity)을 고려해 부지특성조사를
정밀히 수행하고 추적자 시험을 통해 종분산계수를 비교적 정확하게 추정해야 할 것으로 판단된다.
3.3. 반응 변수 변화에 따른 반응성
물질의 거동
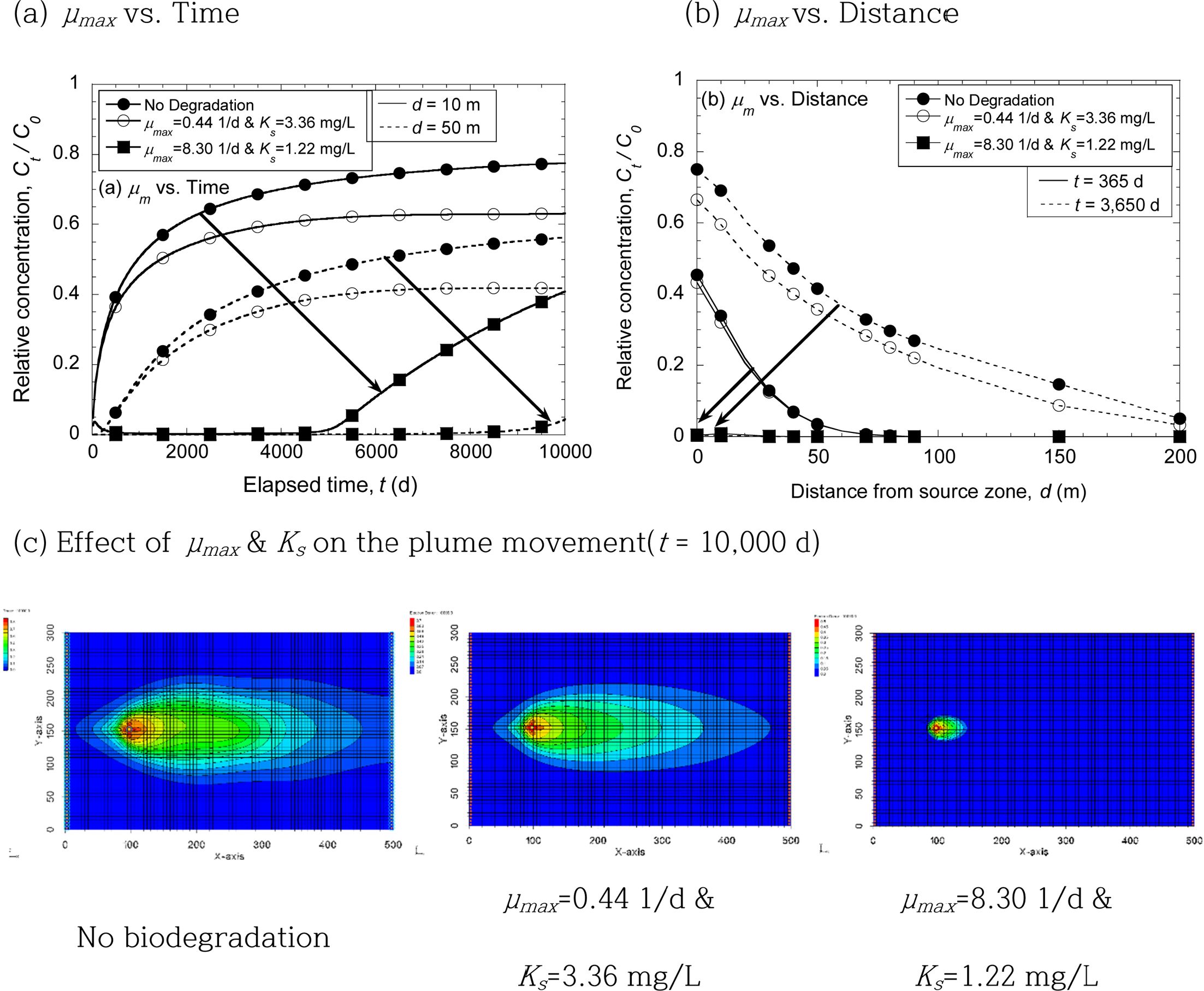
지하수 내 용해된 BZ 거동(fate)에 주요한 영향을 미치는 반응 변수 중 Double monod kinetics의 미생물 성장계수(μm
& Kc)의 변화에 따른 BZ의 시공간에 따른 농도 변화는 Fig. 5(a)와 5(b)에 제시되었으며,
10,000일이 경과 후 모델 도메인 내 오염운의 변화는 Fig. 5(c)에 제시되었다. 기존 연구에서는 유기오염원으로 오염된 지하수에서는 용존산소
농도가 쉽게 고갈되어 호기성 미생물보다는 혐기성 미생물에 의한 분해가 효과적이라고 보고되기도 하나(Mancini et al., 2003), 미생물
컨소시엄 내 복잡한 상호작용으로 인해 미생물의 성장 kinetics와 BZ 분해효율을 정확하게 정량화하기 매우 어려움이 있다
(Trigueros et al., 2010). 따라서, 본 연구에서는 실제 지하수 내 이류와 확산에 의한 미생물의 이송과 동시에 성장을 고려해 호기성 미생물의
성장 kinetics과 지하수 내 이송과 탈부착을 모사함과 동시에 BZ 생분해를 예측하였다.
생분해를 통한 BZ 농도 감소를 일차분해상수로 지수적으로 표현한 1차 분해식(first-order kinetics) 대비 제한 기질인
BZ과 용존산소의 농도변화에 따른 미생물의 성장을 고려한 Double monod kinetics를 활용해 예측한 결과, Double monod
kinetics의 미생물 성장계수(μm & Kc)의 변화에 따라 BZ의 시공간 농도는
크게 변화하는 것으로 조사되었다. 따라서 Double monod kinetics의 미생물 성장계수(μm & Kc)
입력변수 변화에 따라 모델 예측농도는 크게 변화해 예측 농도의 불확실성을 증대시킬 민감도가 높은 변수로 판단된다.
비록 Double monod kinetics를 활용해 BZ 생분해를 예측하는 것이 전자수용체 농도변화 및 미생물의 개체수 등을 고려하지 못하는 1차
분해식 대비 비교적 정확하나, Double monod kinetics의 미생물 성장계수(μm & Kc)와
오염물질 분해 시 성장하는 미생물의 화학양론 수율계수(YX/C) 등의 변수를 현장에서 정확하게 산출하기가 비교적
큰 어려움이 있다.
따라서, Double monod kinetics의 미생물 성장계수(μm & Kc)와
미생물의 화학양론 수율계수(YX/C) 등의 합리적 범위가 제시된 오염물질에 한정해서 활용하는 것이 타당하며, 활용
시 입력변수 변화에 따라 모델 예측결과의 불확실성이 증대될 경우 민감도 분석을 우선 수행할 필요가 있다.
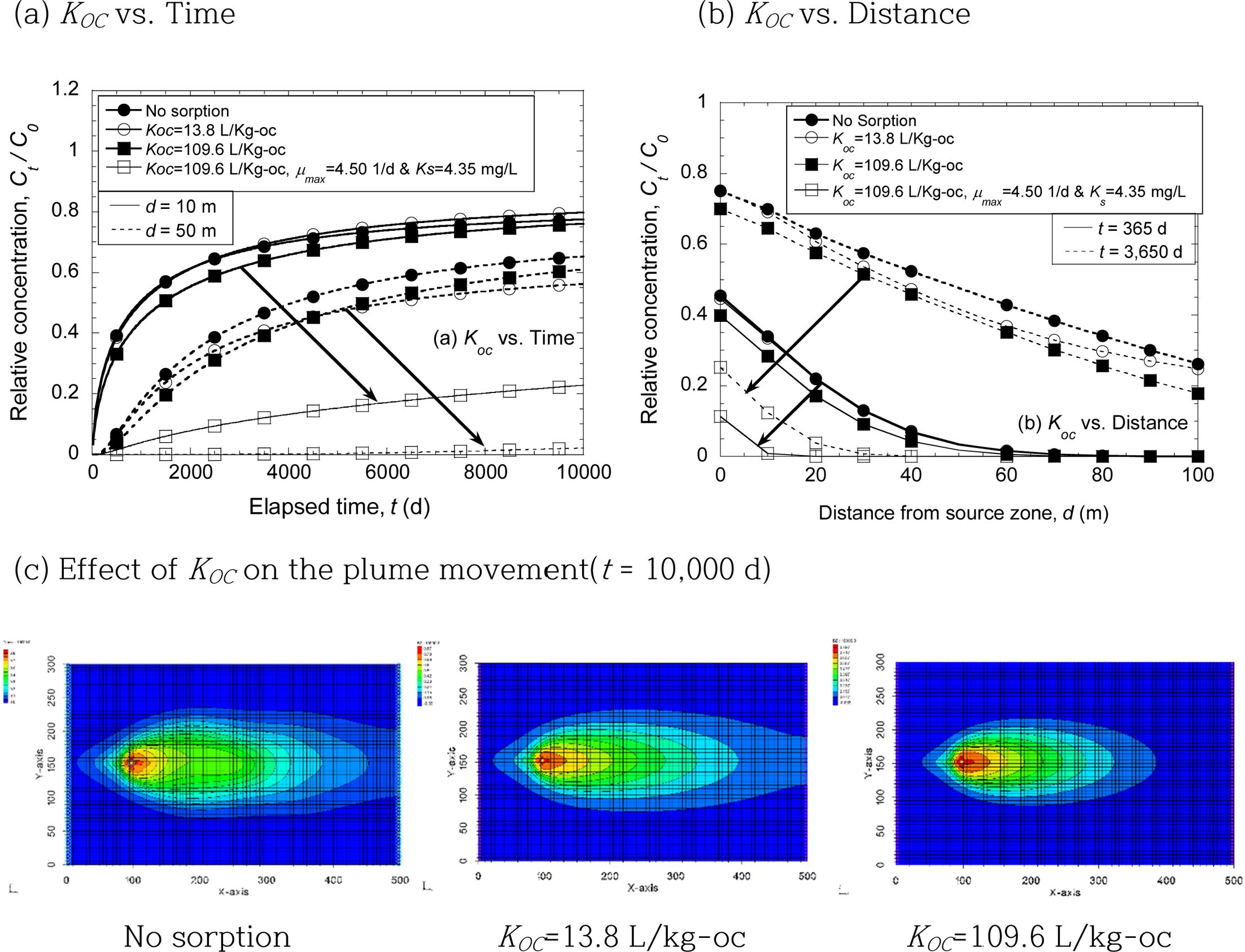
BZ 거동(fate)에 주요한 영향을 미치는 반응 변수 중 수착은 유기탄소기반 수착계수(Koc)를 활용해
비경쟁 선형 수착(noncompetitive & linear sorption)으로 모의하였으며, BZ의 시공간 농도 변화는 Fig.
6(a)와 6(b)에 제시되었으며, 10,000일이 경과 후 모델 도메인 내 오염운의 변화는 Fig. 6(c)에 제시되었다. 선형 수착모형을 활용해
BZ 수착을 예측한 결과, 수착이 증대됨에 따라 BZ의 토양으로 수착량이 증대되고 지하수 내 BZ 이송이 지연되어 농도가 감소되고 오염운의 크기도
감소됨을 확인할 수 있다. 그러나, 수착은 생분해 대비 입력변수 변화에 따른 농도 변화가 비교적 작은 것을 알 수 있으며, 이를 통해 수착 변수가
미생물 성장계수 변수 대비 비교적 민감도가 낮은 것을 알 수 있다.
실제 수착은 지하수의 유동 대비 오염물질의 이동속도를 지연시키며 지하수 내 오염물질 농도를 일부 저감시키는 역할을 하지만, 수착된 오염물질이
탈착되거나 수착이 포화상태에 도달 시 오염물질은 지하수와 함께 다시 이송되므로 지하수에서 오염물질 제거가 영구적이지 않으며 단지 이동을 지연시킬
뿐이다(Joo et al., 2008; 2011; 2012). 그러나, 대부분의 지중환경에서 수착과 생분해가 동시에 발생하는 것을 고려 시,
BZ 농도는 수착과 생분해를 통해 비반응성 물질 대비 매우 낮은 농도로 예측되었으며, 이를 통해 수리동역학적 변수 대비 반응 변수의 영향이
BZ 거동을 설명할 때 지배적인 영향을 미치는 것을 알 수 있다.
현장 부지조사에서 대수층 내 유기물과 점토광물의 비율(fraction)이 높은 경우, 각각 유기오염물질과 무기오염물질의 수착이 증가해
비교적 장시간 오염물질 이동을 지연시킬 수 있다. 따라서, 실제 현장 부지의 미세 공극(micro-scale)에서 대수층 크기(mega-scale)까지
정밀하게 수행된 부지특성조사를 통해 유기물과 점토광물의 비율과 분포상태 등을 비교적 정확하게 조사해야 할 것으로 판단된다.
3.4. 기본 사례 대비 농도차의
시공간적 분석
모델의 입력변수 변화에 따라 각 사례와 기본 사례 예측농도의 정량적 차이를 시공간적으로 분석하기 위해 수리동역학적 변수와 반응 변수의
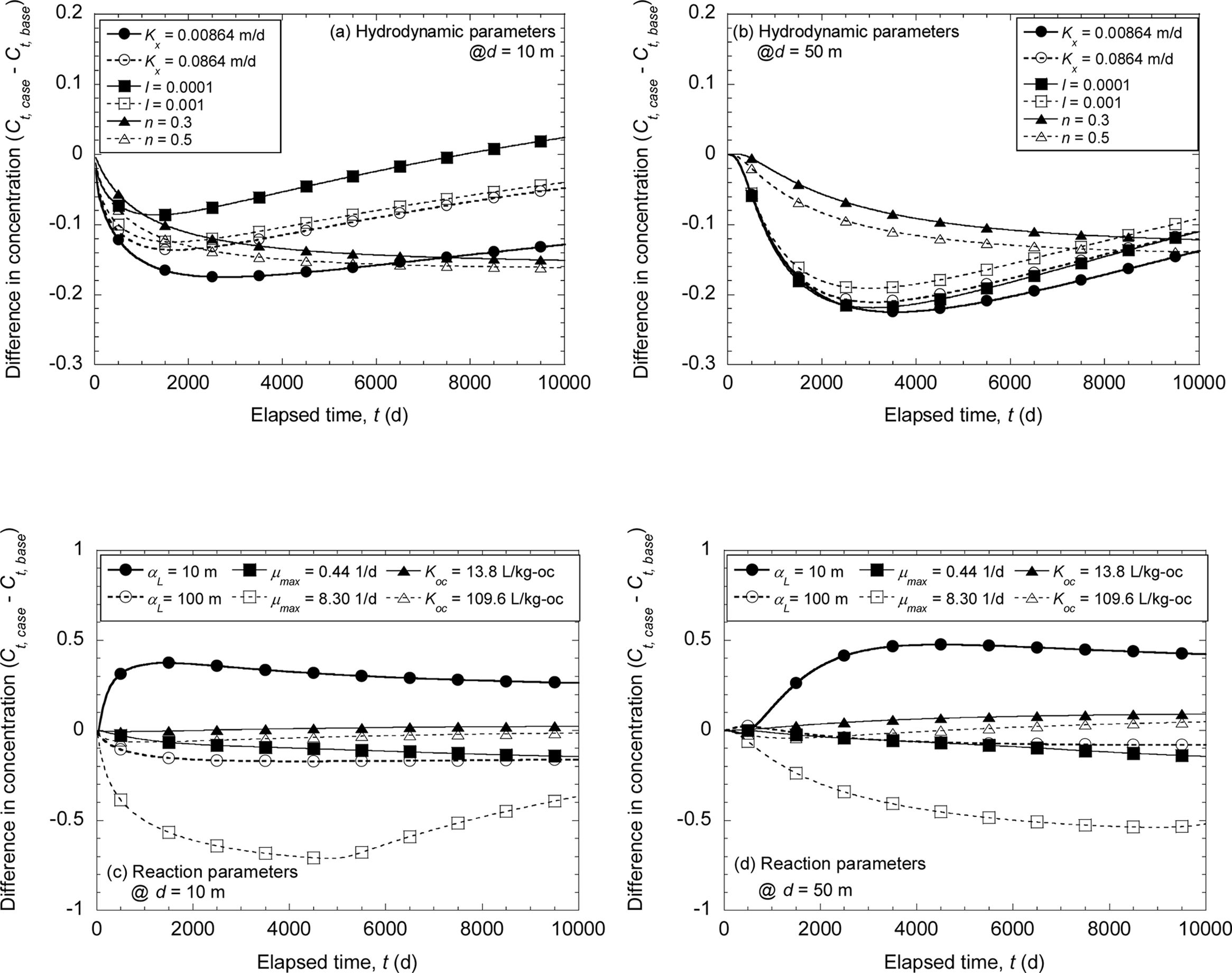
변화에 따라 예측농도의 차이를 시공간에 따라 분석하였다. 비교적 농도차가 큰 종분산계수(αL)는 반응 변수에 포함시켜
두 개의 관측정(d=10 m, 50 m)에서 시간 경과에 따라
분석한 결과는 Fig. 7에 제시되었다. 투수계수와 수리학적 구배의 감소에 따라 두 관측정에서 각 사례의 예측농도는 기본 사례 대비 감소하므로
농도차는 점차 증대되며, 오염운의 이동에 의해 최대 농도차가 발생하는 시간은 두 개의 관측정에서 다른 것으로 분석되었다. 즉, 투수계수와 수리학적
구배가 낮은 경우 지하수 이류에 의한 오염물질 이송이 감소하며, 오염운의 이동에 따라 시공간별로 다른 농도차를 나타냄을 알 수
있다. 반면에, 유효공극률 변화는 오염물질 이송에 큰 영향을 미치지 않으며, 시공간별로 큰 농도차를 나타내지 않음을 알 수 있다.
종분산계수가 감소하면 수리동역학적 분산이 감소되어 오염원 주변과 원거리에서 기본 사례대비 농도차가 크게 증가하는 반면, 종분산계수가
증가하면 오염물질 질량의 확산으로 오염원 주변과 원거리에서 농도차가 감소하는 경향을 나타냈다. 또한, 미생물 성장계수가 증가함에 따라 주입된 오염물질이
생분해되어 오염물질 질량 변환 및 제거가 발생해 반응 기작이 없는 기본 사례 대비 매우 낮은 농도로 예측되었다. 수착계수가 증가함에 따라 주입된
오염물질이 토양에 수착되어 기본 사례 대비 농도차는 증가하였으나, 생분해계수 대비 수착계수 변화에 따른 농도차는 매우 미미한 것으로 분석되었다.
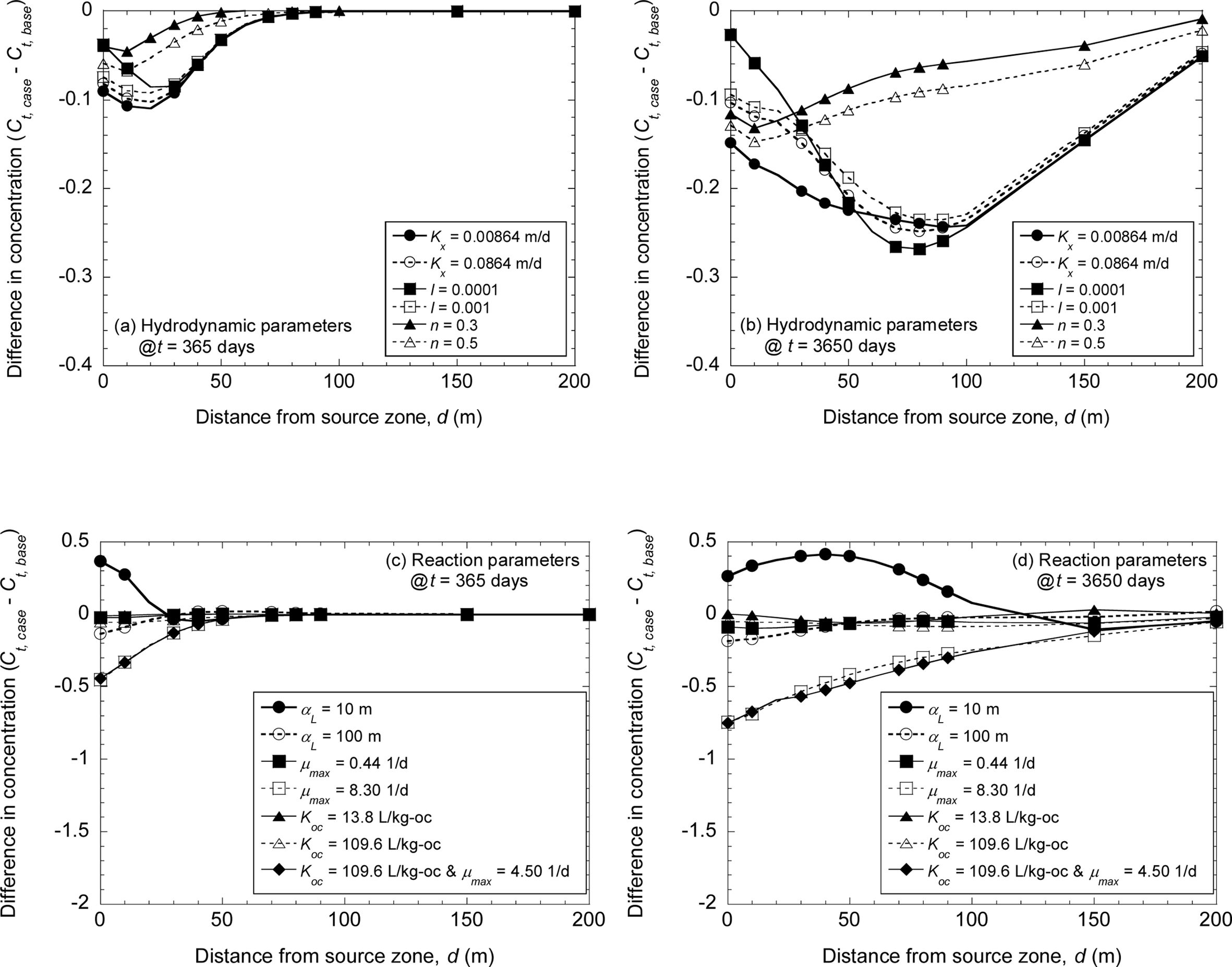
오염물질이 주입정에 지속 주입 시 수리동역학적 변수와 반응 변수의 변화에 따라 1년(365일)과 10년(3,650일)이 경과 후 각
사례와 기본 사례의 농도차를 오염원에서 지하수 이동 거리에 따라 분석한 결과는 Fig. 8에 제시되었다. Fig. 7과 동일하게 투수계수와 수리학적
구배의 감소에 따라 농도차는 점차 증대되며, 오염운의 이동에 의해 최대 농도차가 발생하는 거리는 경과 시간에 따라 다른 것으로 분석되었다. 즉,
투수계수와 수리학적 구배의 변화는 오염운의 이동에 비교적 큰 영향을 미쳐 시공간별로 매우 다른 농도차를 나타내는 반면 유효공극률의 변화는 오염운의
이동에 큰 영향을 미치지 않아 최대 농도차가 발생하는 시공간이 투수계수와 수리학적 구배와는 다른 것으로 조사되었다.
Fig. 8에 제시된 분산계수와 생분해계수 변화에 따른 예측농도의 변화는 큰 차이를 나타내며, Fig. 8에 제시된 분산계수와 생분해계수
변화에 따른 예측농도의 변화는 큰 차이를 나타내며, 분산계수 변화에 따른 기본 사례 대비 농도차는 오염운 중심 이동에 의해 결정되어 이동거리에
따라 최대 농도차가 발생하는 반면, 생분해계수와 반응계수의 변화는 오염운 이동 보다는 주입정에서부터 오염물질 질량 변환 및 제거가 주요 기작으로
이동거리 보다는 주입정에서 최대 농도차가 발생하였다. 또한, 지중환경에서 자연저감(natural attenuation) 기작인 생분해와
수착이 동시에 발생하는 경우, 오염물질의 예측농도가 가장 낮게 예측되었으며, 오염물질 질량 감소는 오염원부터 지속적으로 발생해 기본 사례 대비
가장 큰 농도차가 발생함을 알 수 있다.
3.5. 모델 입력변수들의 민감도
평가
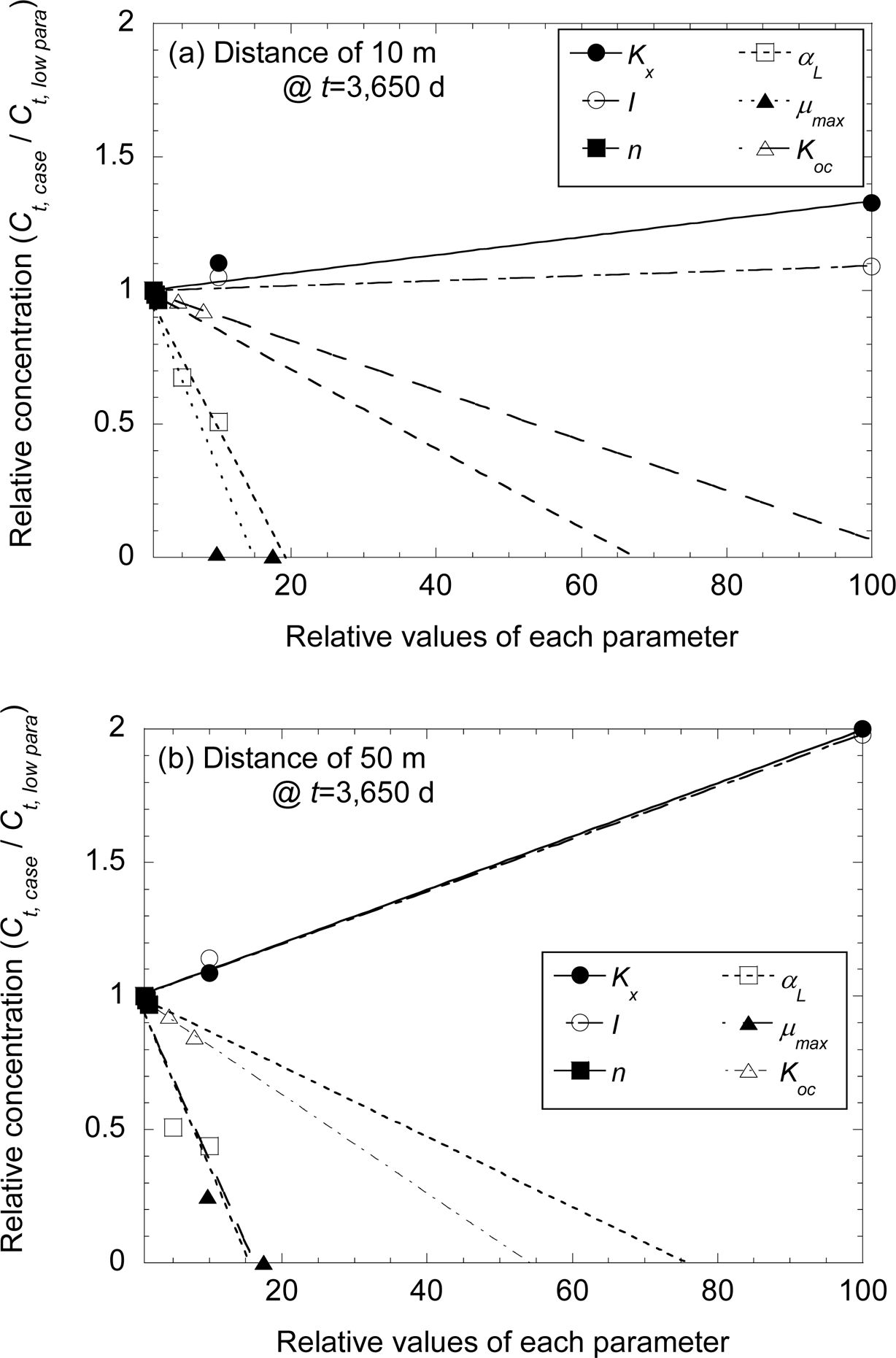
모델 입력변수들의 상대적 변화에 따른 오염물질 예측농도의 변화를 정량적으로 평가하기 위해, 두 개의 관측정(d=10 m, 50 m)에서 예측농도의 상대적
변화를 Fig. 9에 제시하였다. 기존 연구(Hamby, 1994)에서 회귀분석(regression analysis)이 복잡한 민감도 분석 모델과
가장 유사한 분석결과로 판명되었으므로, 본 연구에서는 모델 입력변수의 변화에 따른 예측농도의 상대적 변화를 회귀분석한 결과 개략 선형(approximate
linear)으로 변화하였으며, 민감도의 정량적 평가를 위해 y 절편은 1.0으로 고정한 선형 회귀식을 산출해 기울기의 절대값을
sensitivity index(SI)로 산출하였다. Fig. 9a와 9b는 두 개의 관측정(d=10 m, 50 m)에서 10년이 경과 후
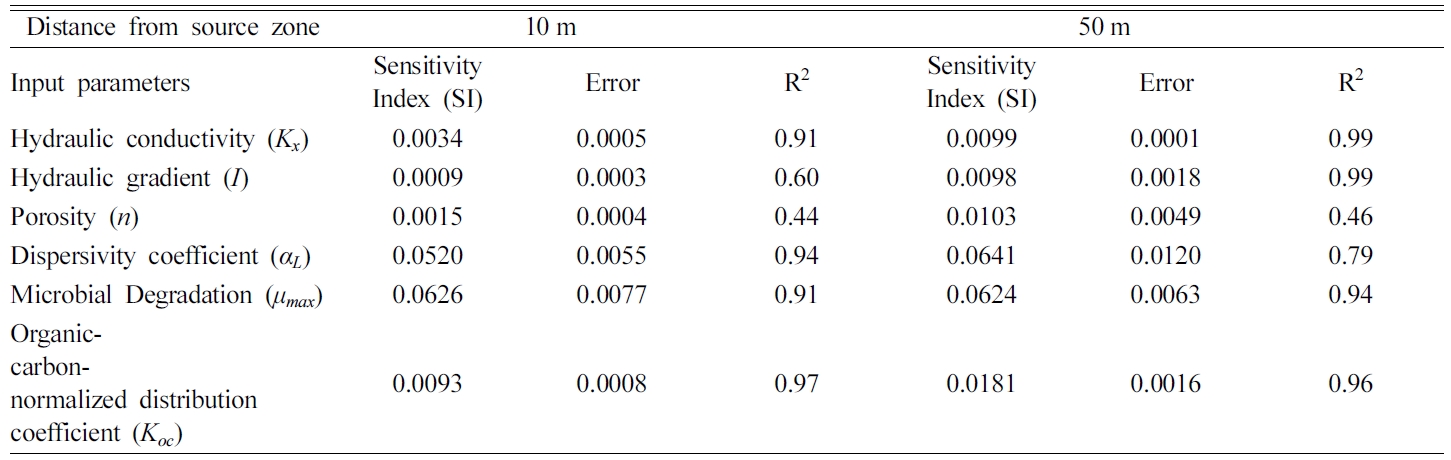
각각 민감도의 분석 결과이며, Table 2는 각 입력변수의 sensitivity index를 정리하였다.
주입정 주변의 오염원에 가까운 관측정(d=10 m)의 경우, 민감도가 큰 변수로는
생분해계수와 종분산계수로 조사되었으며 생분해계수와 종분산계수가 증가함에 따라 각각 오염물질 질량이 감소하거나 수리동역학적 분산을 통한 희석으로
인해 오염물질 농도는 급격히 감소하는 경향이 관측되었다. 반면에 수착계수의 증가는 오염물질 질량의 액상에서 토양으로 물질전달을 증가시켜 오염물질
농도가 점진적으로 감소하는 경향을 나타냈으며, 투수계수와 수리학적 구배가 증가함에 따라 지하수의 이류에 의한 오염물질 이송이 촉진되어 오염물질
농도의 점진적 증가를 유도한 반면, 유효공극률 증가는 지하수 유속 감소에 따라 오염물질 농도의 점진적으로 감소시켰다. 그러나, 이러한 변수들은
생분해계수와 종분산계수 대비 입력변수들의 변화에 따른 오염원 주변의 오염물질 농도 변화에 큰 영향을 미치지는 않는 것으로 분석되어 비교적 민감도가
낮은 변수로 판단된다.
주입정 주변의 오염원에 가까운 관측정(d=10 m)의 경우와 유사하게 오염원에서
비교적 원거리에 위치한 관측정(d=50 m)의 경우, 민감도가 큰
변수로는 종분산계수와 생분해계수로 조사되었으며, 종분산계수와 생분해계수의 변화에 따라 원거리에서 오염물질 농도가 크게 변화하는 것으로 분석되었다.
즉 오염원 주변에서부터 지속적으로 발생하는 생분해 대비, 종분산계수는 오염원 주변보다는 수리동역학적 분산을 통한 희석의 기작으로 원거리의 오염물질
농도 변화에 더 큰 영향을 끼치는 것으로 조사되었다.
생분해계수를 제외하고는 모든 입력변수가 오염원에 가까운 관측정(d=10 m) 대비 비교적 원거리에
위치한 관측정(d=50 m)에서 민감도가 증대되었으며, 이를 통해 입력변수의 민감도는 지하수의
이동거리에 따라 변경되며 오염원 주변보다는 원거리에서 오염물질 거동에 미치는 영향이 더욱 증가하고 있음을 의미한다. 특히, 반응 변수 대비 수리동역학적
변수인 투수계수, 수리학적 구배, 유효공극률의 민감도가 오염원과 거리가 증대됨에 따라 상대적으로 크게 증가하는 것으로 조사되어 오염원과 원거리에서
오염물질 농도를 결정 시에 주요한 영향을 미칠 수 있을 것으로 판단된다.
전체적으로 종분산계수와 생분해계수 그리고 수착계수의 입력변수 변화가 오염물질 예측농도에 비교적 큰 영향을 미치는 반면, 투수계수와 수리학적
구배 및 유효공극률의 입력변수 변화는 상대적으로 미미한 영향을 미치는 것으로 조사되었다. 하지만, 이러한 수리동역학적 변수와 반응 변수의 민감도
지수는 지하수의 이동 거리 및 시간에 따라서 변화하며, 일부 수리동역학적 변수(예, 유효공극률과 투수계수)들은 상호영향을 미치며 독립적이지 않은
것으로 조사되었다. 결론적으로, 입력변수의 변화에 따른 모델 결과의 불확실성을 개념 모델을 통해 사전에 정량화하여 모델 결과에 가장 큰 영향을
미치는 민감도가 높은 입력변수 들을 부지특성에 적합하게 정밀 조사할 필요가 있다고 판단된다.
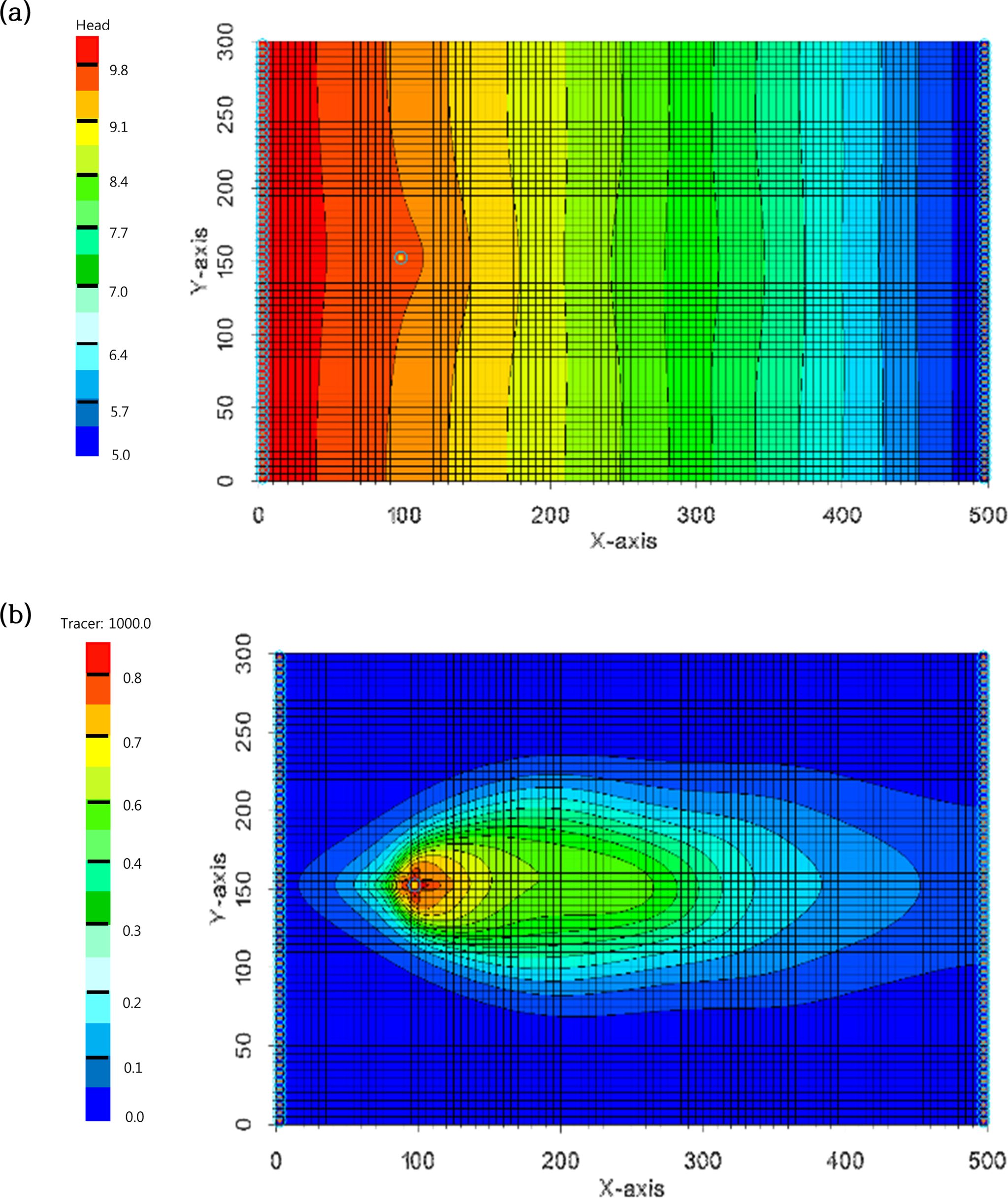
|
Fig. 2 Simulation results for base case scenario. (a) Head distribution of groundwater in steady state, and (b) contour plot of conservative compound at t = 10,000 d. |
|
Fig. 3 Effect of hydrodynamic input parameters on the concentration of nonreactive compound in terms of both elapsed time and distance from source zone. |
|
Fig. 4 Effect of longitudinal dispersivity on the concentration and plume of nonreactive compound in terms of both elapsed time and distance from source zone. |
|
Fig. 5 Effect of microbial degradation on the concentration and plume of benzene in terms of both elapsed time and distance from source zone. |
|
Fig. 6 Effect of sorption on the concentration and plume of benzene in terms of both elapsed time and distance from source zone. |
|
Fig. 7 Difference in concentration (unit: mg/L) of between specific case and base case at two different observation wells in terms of the elapsed time. |
|
Fig. 8 Difference in concentration (unit: mg/L) between specific case and base case at two different times in terms of the distance from the source zone. |
|
Fig. 9 Sensitivity index of each input parameter at two different observation wells after 10 years. |
|
Table 2 Summary of sensitivity index and ranking for hydrodynamic and reaction parameters to estimate the fate and transport of contaminant at the distance of 10 and 50 m from the source zone after 10 years |
우리나라 대수층의 수리리질학적 특성을 반영한 개념 모델(conceptual model)을 설정해 지하수 유동과 오염물질 거동을 예측
시 수리동역학적 변수(투수계수, 수리학적 구배, 유효공극률, 분산)와 반응 변수(수착, 분해)의 민감도 분석을 통해 입력변수의 변화에 따른 예측농도의
불확실성을 조사하였다. 수리동역학적 변수 중 투수계수, 수리학적 구배와 유효공극률은 변수 값이 변화함에 따라 오염물질이 특정 관측점에 도달하는
시간에 영향을 미치나, 장기간 오염물질이 주입되는 경우 수렴 농도 값은 동일한 반면, 종분산계수는 변수 값이 변화함에 따라 오염물질이
특정 관측점에 도달하는 시간에 영향을 미치며 수렴 농도 값의 차이도 유발한다. 수리동역학적 변수 대비, Double monod kinetics의
미생물 성장계수(μm & Kc) 변화에 따라 모델 예측농도는 크게 변화해 예측결과의
불확실성을 증대시킬 가능성이 높은 변수로 판단되며, 수착은 미생물에 의한 생분해 대비 입력변수 값의 변화에 따른 농도 변화가 비교적 작은 것으로
조사되었다.
종분산계수는 오염운 이동과 농도 분포에 가장 큰 영향을 미치는 변수이며, 생분해계수는 오염운 이동과 동시에 오염물질 질량 변환 및 제거가
발생해 농도 저감이 가장 활발하였다. 전체적으로 종분산계수와 생분해계수 그리고 수착계수의 입력변수 변화가 오염물질 예측농도에 비교적 큰 영향을
미치는 반면, 투수계수와 수리학적 구배 및 유효공극률의 입력변수 변화는 상대적으로 미미한 영향을 미치는 것으로 조사되었다. 하지만, 이러한 수리동역학적
변수와 반응 변수의 민감도 지수는 지하수의
이동 거리(시간)에 따라서 변화하므로, 입력변수의 변화에 따른 모델 결과의 불확실성을
사전에 개념 모델을 설정해 정량화하여 모델 결과에 가장 큰 영향을 미치는 민감도가 높은 입력변수 들을 부지특성에 적합하게 선별적으로 조사할 필요가
있다고 판단된다.
본 연구는 환경부의 재원으로 한국환경산업기술원의 지중환경오염위해관리기술개발사업의 지원을 받아 연구되었습니다(과제번호
2018002450004).
- 1. Atlabachew, A., Shu, L., Wu, P., Zhang, Y., and Xu, Y., 2013, Numerical modeling of solute transport in a sand tank physical model under varying hydraulic gradient and hydrological stresses. Hydrogeol. J., 26(6), 2089-2113.
-

- 2. Bailey, R.T., Morway, E.D., Niswonger, R.G., and Gates, T.K., 2013, Modeling variably saturated multispecies reactive groundwater solute transport with MODFLOW-UZF and RT3D, Ground water, 51(5), 752-716.
-

- 3. Baveye, P. and Valocchi, A., 1989, An evaluation of mathematical models of the transport of biologically reacting solutes in saturated soils and aquifers, Water Resour. Res., 25(6), 1413-1421.
-

- 4. Chang, S.W., Moon, H.S., Lee, E.H., Joo, J.C., and Nam, K.P., 2019, Numerical study of contaminant pathway for risk assessment in subsurface of contaminated sites, J. Soil Groundw. Environ., 24(3), 13-23.
- 5. Chen, Y.M., Abriola, L.M., Alvarez, P.J.J., Anid, P.J., and Vogel, T.M., 1992, Modeling transport and biodegradation of benzene and toluene in sandy aquifer material: Comparisons with experimental measurements, Water Resour. Res., 28(7), 1833-1847.
-

- 6. Clement, T.P., 1999, A Modular Computer Code for Simulating Reactive multi-species Transport in 3-Dimensional Groundwater Systems, Rich land, PNNL-11720.
-

- 7. Clement, T.P., Sun, Y., Hooker, B.S., and Petersen, J.N., 1998, Modeling multispecies reactive transport in ground water, Ground Water Monit. Remed., 18(2), 79-92.
-

- 8. Delle Site, A., 2001, Factors affecting sorption of organic compounds in natural sorbent/water systems and sorption coefficients for selected pollutants, A review, J. Phys. Chem. Ref. Data, 30(1), 187-439.
-

- 9. Essaid, H.I., Bekins, B.A., and Cozzarelli, I.M., 2015, Organic contaminant transport and fate in the subsurface: Evolution of knowledge and understanding, Water Resour. Res., 51(7), 4861-4902.
-

- 10. Fetter, C.W., 2001. Contaminant hydrogeology. Prentice Hall Inc., Upper Saddle River.
- 11. Han, J.S., 2015, Hydrogeology and groundwater modeling, Publishing Co.Naeha, Korea. (In Korean)
- 12. Hamby, D.M., 1994, A review of techniques for parameter sensitivity analysis of environmental models, Environ Monit Assess, 32(2), 135-154.
-

- 13. Joo, J.C., Shackelford, C.D., and Reardon K.F., 2008, Sorption of nonpolar neutral organic compounds to humic acid-coasted sands: Contributions of organic and mineral components, Chemosphere, 70(7), 1290-1297.
-

- 14. Joo, J.C., Shackelford, C.D., and Reardon, K.F., 2011, Sorption of neutral organic compounds in mixtures to mineral surfaces and humic acid-mineral complexes, J. Hazard. Toxic Radioact. Waste., 15(3), 188-198.
-

- 15. Joo, J.C., Shackelford C.D., and Reardon, K.F., 2012, Lumping analysis for sorption of neutral organic compounds in mixtures to simulated aquifer sorbents, J. Environ. Eng., 138(5), 552-561.
-

- 16. Kim, M.J. and Park, J.W., 2007, Contaminant fate and transport modeling for risk assessment, J. Soil Groundw. Environ., 12(1), 44-52.
- 17. Lapworth, D.J., Baran, N., Stuart, M.E., and Ward, R.S., 2012, Emerging organic contaminants in groundwater: A review of sources, fate and occurrence, Environ. Pollut., 163, 287-303.
-

- 18. Macini, S.A., Ulrich, A.C., Lacrampe-Couloume, G., Sleep, B., Edwards, E.A., and Lollar, B.S., 2003, Carbon and hydrogen isotopic fractionation during anaerobic biodegradation of benzene, Appl. Environ. Microbiol., 69(1), 191-198.
-

- 19. Mackay, D.M., Roberts, P.V., and Cherry, J.A., 1985, Transport of organic contaminants in groundwater, Environ. Sci. Technol., 19(5), 384-392.
-

- 20. McDonald, M.G. and Harbaugh, A.W., 1988, A Modular Three dimensional Finite-difference Ground-water flow model: Techniques of Water-Resources Investigations of the U.S. Geological Survey, Book 6, Chapter A1.
- 21. Na, H.N., Koo, M.H., Cha, J.H., and Kim, Y.J., 2007, Sensitivity analysis of groundwater model predictions associated with uncer-tainty of boundary conditions: A case study, J. Soil Groundw. Environ., 12(3), 53-65.
- 22. Oh, Y.S., Shareefdeen, Z., Baltzis, B.C., and Bartha, R., 1994, Interactions between benzene, toluene, and p-Xylene (BTX) during their biodegradation, Biotechnol. Bioeng., 44(4), 533-538.
-

- 23. Park, D.H., Koo, M.H., and Kim, Y.C., 2015, Hydro-thermal numerical simulation for an artificial recharge test in a fractured rock aquifer, J. Soil Groundw. Environ., 20(1), 65-75.
-

- 24. Site, A.D., 2000, Factors affecting sorption of organic compounds in natural sorbent/water systems and sorption coefficients for se-lected pollutants. A Review, J. Phys. Chem. Ref. Data, 30(1), 187-439.
-

- 25. Song, X., Zhang, J., Zhan, C., Xuan, Y., and Ye, M., and Xu, C., 2015, Global sensitivity analysis in hydrological modeling: Review of concepts, methods, theoretical framework, and applications, J. Hydrol., 523, 739-757.
-

- 26. Trigueros, D.E.G., Modenes, A.N., Kroumov, A.D., and Espinoza-Quinones, F.R., 2010, Modeling of biodegradation process of BTEX compounds: Kinetic parameters estimation by using particle swarm global optimizer, Process Biochem., 45(8), 1355-1361.
-

- 27. USEPA, 1996, Soil Screening Guidance: Technical Background Document, Second edition, Office of solid waste and emergency response, Washington, DC. EPA/540/R95/128.
- 28. ASTM, 1999, RBCA Fate and Transport Models: Compendium and Selection Guidance, West Conshohocken, PA.
- 29. Zheng, C. and Gordon, D.B., 2002, Applied Contaminant Transport Modeling. John Wiley & Sons.
 This Article
This Article
-
2020; 25(1): 37-52
Published on Mar 31, 2020
- 10.7857/JSGE.2020.25.1.037
- Received on Feb 13, 2020
- Revised on Mar 2, 2020
- Accepted on Mar 13, 2020
 Services
Services
Shared
 Correspondence to
Correspondence to
- Hee Sun Moon
-
Groundwater Research Center, Korea Institute of Geoscience and Mineral Resources
- E-mail: hmoon@kigam.re.kr





